Предмет: Алгебра,
автор: lenamokrousova201257
Число X отмечено на координатной прямой. Сравните числа A = 1 + 1/x и B = 1 - 2/x с нулём.
Приложения:
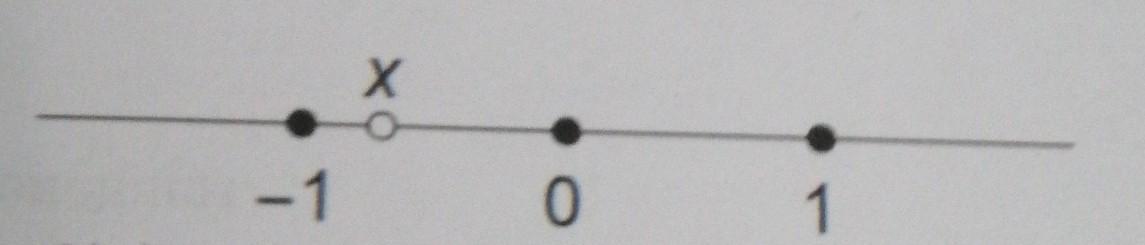
Ответы
Автор ответа:
8
Ответ:
A < 0; B > 0
Объяснение:
Так как -1 < x < 0 по условию, то 1/x < -1, а следовательно A = 1 + 1/x < 1 - 1, то есть A меньше 0.
Продолжая рассуждение, получаем, что -1/x > 1, поэтому -2/x > 2 (умножаем обе части неравенства на 2), а следовательно B = 1 - 2/x = 1 + (-2/x) > 1 + 2 > 0, то есть B больше 0.
Автор ответа:
5
Ответ:
A<0 и B>0
Объяснение:
Из чертежа определяем:
-1 < x < 0.
Тогда
-1 < x ⇒ x+1 > 0
и
x < 0 ⇒ x-2 < -2 < 0.
Далее, из x<0, x+1>0 и x-2<0 следует:
Похожие вопросы
Предмет: Физика,
автор: khantore6
Предмет: Геометрия,
автор: Аноним
Предмет: Математика,
автор: momoring02
Предмет: Математика,
автор: MishutkaAly