Предмет: Математика,
автор: sashaberezovski8
Решите пожалуйста этот пример. Даю 18 баллов
Приложения:
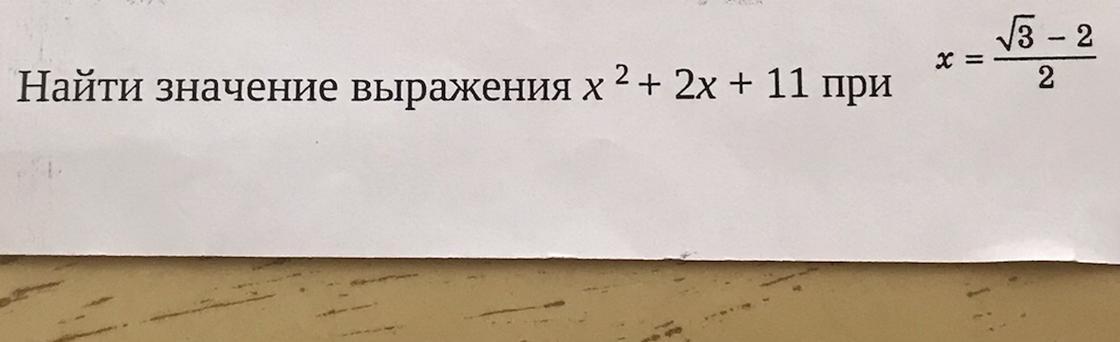
Ответы
Автор ответа:
2
Решение.
Применяем формулы: .
Автор ответа:
0
Відповідь: 10,75
###########
Приложения:

Похожие вопросы
Предмет: Окружающий мир,
автор: znayu99ru
Предмет: Английский язык,
автор: Vessenii
Предмет: Қазақ тiлi,
автор: АринаБогданова
Предмет: История,
автор: SashaKusa