Предмет: Математика,
автор: StaVoz6699
Решение пожалуйста, дифференциальные уравнения
Приложения:
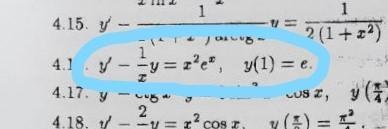
Ответы
Автор ответа:
1
Умножим обе части уравнения на , мы получим
Проинтегрируем обе части уравнения:
Интеграл в последнем уравнении стоящий справа решим по частям
Получили общее решение.
Найдём теперь частное решение, подставив начальные условия.
Частное решение:
Похожие вопросы
Предмет: Математика,
автор: maranaandrusko8
Предмет: Математика,
автор: kobrinaleksandra73
Предмет: Математика,
автор: rkia978
Предмет: История,
автор: Dondiablo44444444