Предмет: Математика,
автор: Dontask
Написать уравнение касательной, проведенной к графику данной функции параллельно данной прямой. Если таких касательных две, привести уравнение только одной из них.
Приложения:
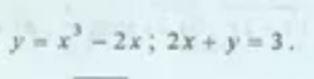
Simba2017:
уравнение можно и покрупнее было написать
х в кубе если что
распишу
буду очень признательна)
Ответы
Автор ответа:
1
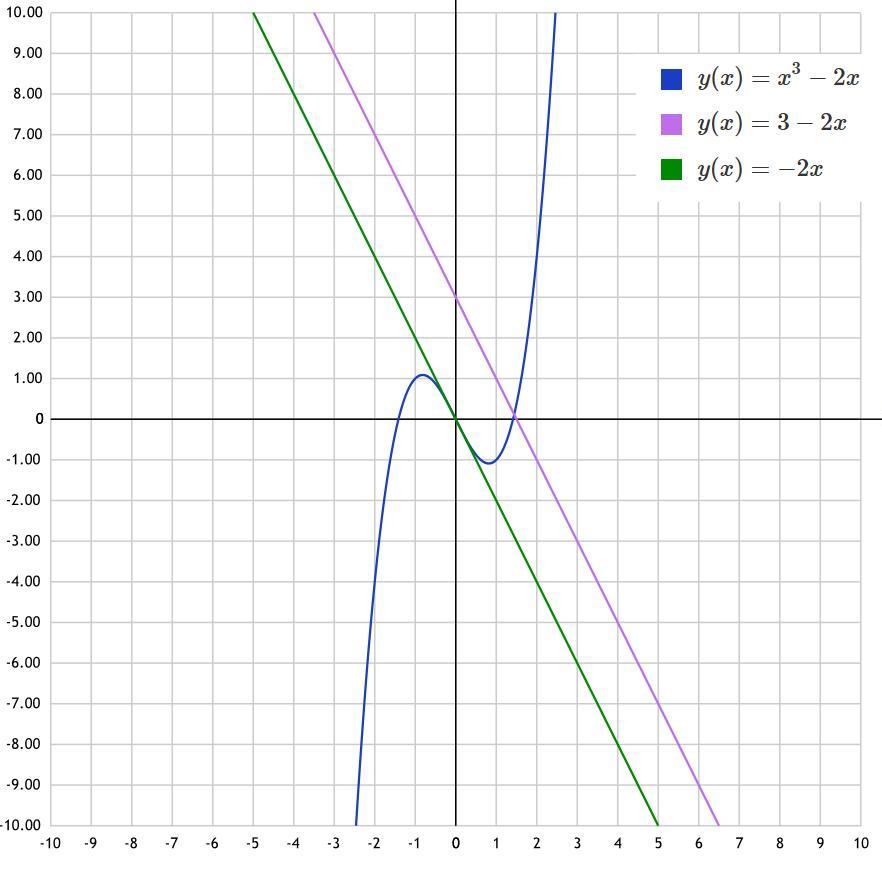
угол наклона касательной такой же как у данной прямой y=3-2x.- это "-2", коэффициент перед х. Он равен производной функции в точке касания, поэтому я найду производную и приравняю ее к -2- тем самым я найду точку касания
y`(x)=3x^2-2=-2
x=0
y(0)=0^3-2*0=0
(0;0)-точка касания искомой прямой и кубичной параболы
Если касательная параллельна прямой y=3-2x, значит она имеет вид
y=-2x+c, чтобы определить с, я в ее уравнение подставлю точку касания, так как точка касания принадлежит касательной тоже
0=-2*0+с; c=0
y=-2x-уравнение искомой касательной
Приложения:
Похожие вопросы
Предмет: Физика,
автор: nastia859
Предмет: Физика,
автор: nastia859
Предмет: Геометрия,
автор: tigranunjyan
Предмет: Математика,
автор: мария1760
Предмет: Математика,
автор: aialinakol