Найдите площадь фигуры, образованной точками(x,y) декартовой плоскости , координаты которых удовлетворяют неравенству  . Ответ округлите до сотых
. Ответ округлите до сотых
Ответы
Ответ:
1142 кв. единица
Пошаговое объяснение:
Дано множество заданное неравенством:
x²+y²+20·(x-|y|)≤0
Неравенство содержит модуль, поэтому рассмотрим случаи в зависимости от знака переменного y.
1) y<0. В силу этого |y| = -y. Тогда неравенство имеет вид:
x²+y²+20·(x-(-y))≤0
x²+2·10·x+100-100+y²+2·10·y+100-100≤0
(x+10)²+(y+10)²≤200
(x+10)²+(y+10)²≤(10·√2)²
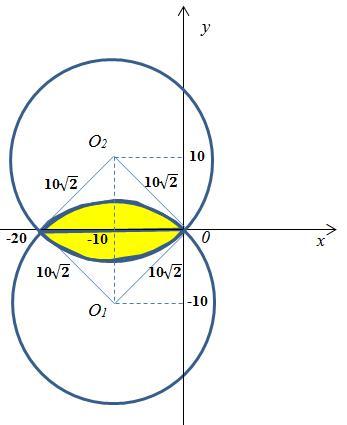
Отсюда следует, что наша фигура - это круг с центром в точке (-10; -10) и радиусом R=10·√2 (R²=200), у которого отделена часть из-за y<0 в виде сегмента (см. рисунок 1, сегмент - жёлтый). Площадь S(y<0) этой фигуры можно определить как разность площадей круга и сегмента:
S(y<0)=Sкруг-Sсегмент=π·R²-Sсегмент=200·π-Sсегмент
Формула площади сегмента:
Sсегмент=
Так как О₁0 является диагональю квадрата стороной 10, то половина угла α=45°, то есть α=90°. Тогда
Sсегмент=
Отсюда:
S(y<0)=200·π-(50·π-100)=200·π-50·π+100=150·π+100 кв. единица.
2) y≥0. В силу этого |y| = y. Тогда неравенство имеет вид:
x²+y²+20·(x-y)≤0
x²+2·10·x+100-100+y²-2·10·y+100-100≤0
(x+10)²+(y-10)²≤200
(x+10)²+(y-10)²≤(10·√2)²
Отсюда следует, что эта фигура тоже круг с центром в точке (-10; 10) и радиусом R=10·√2 (R²=200), у которого отделена часть из-за y≥0 в виде сегмента (см. рисунок 2, сегмент ниже оси Ох - жёлтый). Площадь S(y≥0) этой фигуры также определяется как разность площадей круга и сегмента. Поэтому как и выше получаем:
S(y≥0)=150·π+100 кв. единица.
Теперь сложив оба площади находим площадь фигуры, заданной неравенством x²+y²+20·(x-|y|)≤0:
S=S(y<0)+S(y≥0)=150·π+100+150·π+100=300·π+200 кв. единица.
Если положить, что π=3,14, то
S=300·3,14+200 кв. единица= 1142 кв. единица