Question

Решите задачу
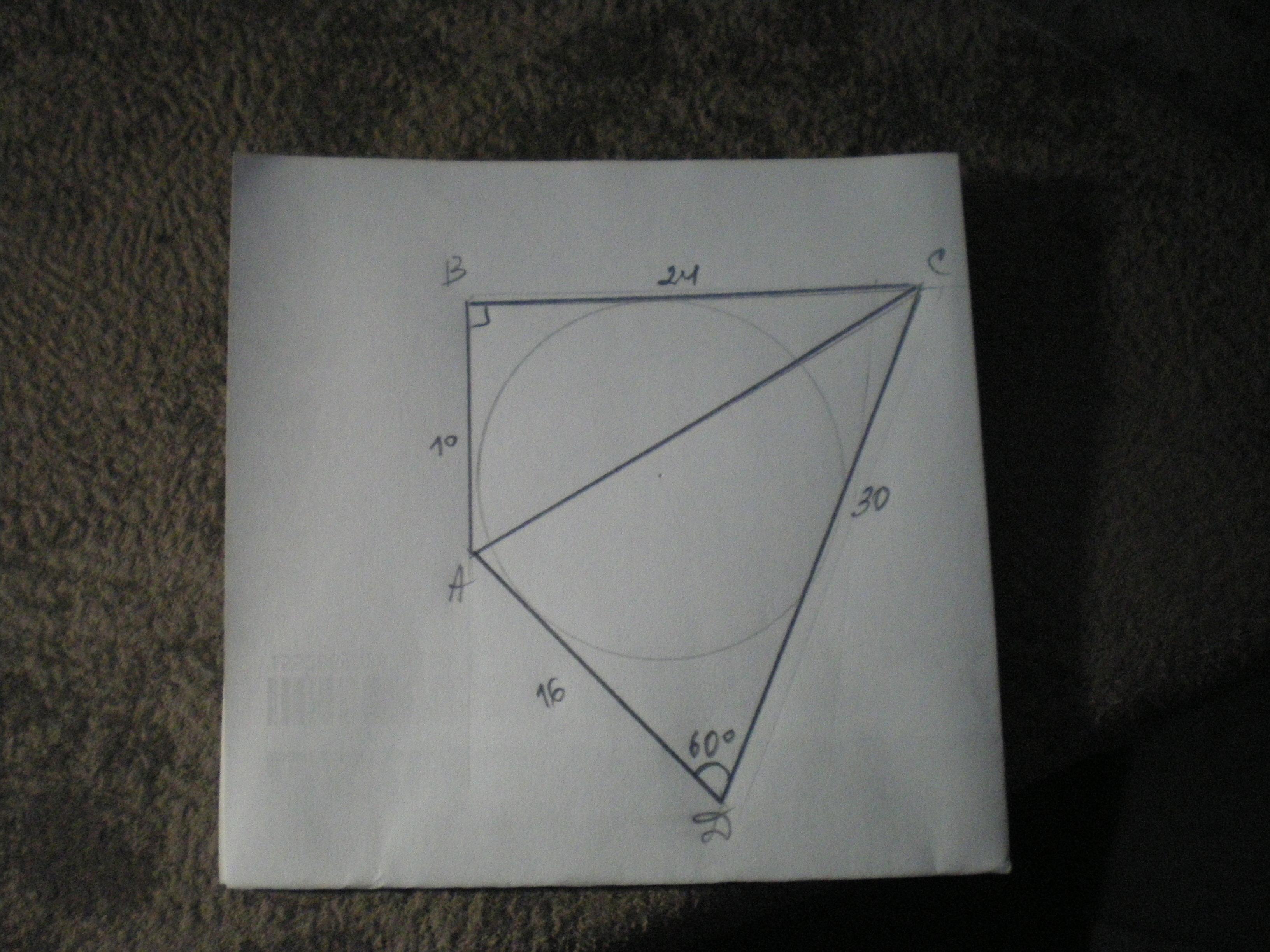
четырёхугольник ABCD описан около окружности, найдите AB и BC, если угол ABC равен 90 градусов, угол ADC равен 60 градусов, AD равно 16 см, CD равно 30 см

Answer 1

Ответ:

24 см и 10 см.

Объяснение:

Если в четырехугольник можно вписать окружность, то суммы длин его противоположных сторон равны.

АВ+СD=АD+ВС

Проведем АС; ΔАВС - прямоугольный. Найдем АС из ΔАСD по теореме косинусов:

АС²=СD²+АD²-2*СD*АD*cos 60°=256+900-960*1/2=676;

АС=√676=26 см.

Если АВ+30=ВС+16,  то ВС-АВ=14 см;

Пусть ВС=х см, тогда АВ=х-14 см.

По теореме Пифагора АС²=АВ²+ВС²;  676=(х-14)²+х²;

х²+х²-28х+196-676=0

2х²-28х-480=0

х²-14х-240=0

По теореме Виета

х=-10 (не подходит по условию) и х=24.

ВС=24 см;  АВ=24-14=10 см.