Предмет: Математика,
автор: daniilchernush
Помогите пожалуйста решить логарифмические уравнения С ОДЗ
Приложения:
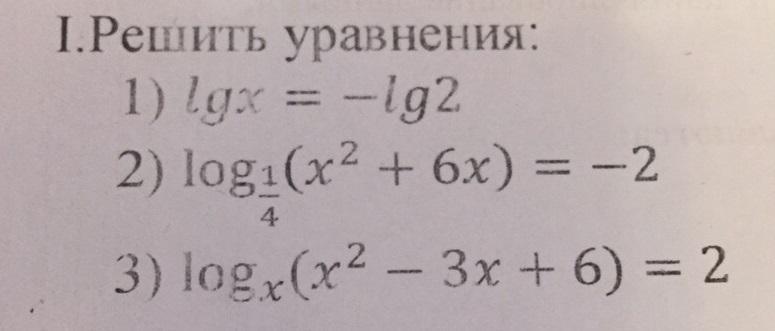
Ответы
Автор ответа:
1
Ответ:
I. 1) lgx = -lg2, ОДЗ: x>0
lgx = lg2⁻¹
x=2⁻¹=1/2=0,5>0
Ответ: {0,5}
2) ОДЗ: x² +6x>0
x² +6x-16=0
D=6²-4•1•(-16)=36+64=100=10²
x₁=(-6-10)/2= -8, (-8)²+6•(-8)=64-48=16>0
x₂=(-6+10)/2=2, 2²+6•2=4+12=16>0
Ответ: {-8 ; 2}
3) ОДЗ: x²-3x+6>0, x>0, x≠1
logₓ(x²-3x+6)=2
logₓ(x²-3x+6)=2•logₓx
logₓ(x²-3x+6)=logₓx²
x²-3x+6=x²
3x=6
x=6:3=2, 2²-3•2+6=4-6+6=4>0, 2>0, 2≠1
Ответ: {2}
axatar:
Я уже решил и только хотел добавить, нет уже удалили вопрос))
спасибо большое, удалили потому что больше трех заданий было
Автор ответа:
1
Ответ:
================================
Пошаговое объяснение:
Приложения:

Похожие вопросы
Предмет: Математика,
автор: svinka114
Предмет: Математика,
автор: stasyagovdik2
Предмет: Геометрия,
автор: dementiaandcourage
Предмет: Математика,
автор: какшка5
Предмет: Биология,
автор: hanum27082005