Предмет: Математика,
автор: Falendrin
Помогите решить срочно, функции
Приложения:
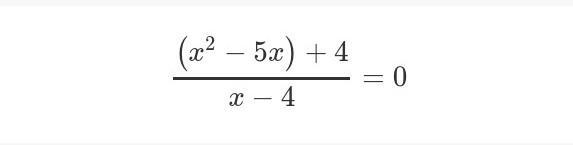
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
Falendrin:
А можно по действиям. 1) Найти область определения функции.. 2) В случае, если область определения функции симметрична относительно начала координат, проверить, не является ли функция четной или не чётной, проверить также не является ли она переодичной. 3) Найти промежутки знакопостоянства функции; выявить поведение функции на каждый промежуток законопостоятельста
Похожие вопросы
Предмет: Математика,
автор: nastiaxxi12
Предмет: Физика,
автор: njalalova405
Предмет: Физика,
автор: njalalova405
Предмет: Алгебра,
автор: SembayE
Предмет: Математика,
автор: 05015