Предмет: Геометрия,
автор: ssburianov
Помогите решить!!! Составьте уравнение плоскости, проходящей через две параллельные прямые.
Приложения:
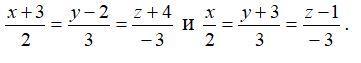
Ответы
Автор ответа:
5
По уравнениям заданных прямых имеем точки на них.
А(-3; 2; -4) и В(0; -3; 1). Вектор АВ(3; -5; 5).
Кроме того, имеем направляющий вектор прямых n = (2; 3; -3).
Нормальный вектор N искомой плоскости будет перпендикулярен векторам АВ и n. Найдём его как векторное произведение.
i j k | i j
3 -5 5 | 3 -5
2 3 -3 | 2 3 = 15i + 10j + 9k + 9j - 15i + 10k =
= 0i + 19j + 19k. Вектор N = (0; 19; 19).
Для составления уравнения плоскости используем формулу:
nx(x - xA) + ny(y - yB) + nz(z - zC) = 0.
Точка А(-3; 2; -4) и вектор N = (0; 19; 19).
Подставим данные и упростим выражение:
0 (x + 3) + 19 (y - 2) + 19(z + 4) = 0
19y - 38 + 19z + 76 = 0
19y + 19z + 38 = 0 .
Похожие вопросы
Предмет: Математика,
автор: Alexxqw46
Предмет: Қазақ тiлi,
автор: Ahmad2802
Предмет: Математика,
автор: TumofeyMudrila
Предмет: Математика,
автор: ильнара14
Предмет: Математика,
автор: Аноним