Question

Вычислить.СРОЧНО$\int\limits^3_0 {f(x)} \, dx , \int\limits^2_0 {f(x)} \,dx =5 и \int\limits^3_2 {f(x)} \, dx=2$

Answer 1

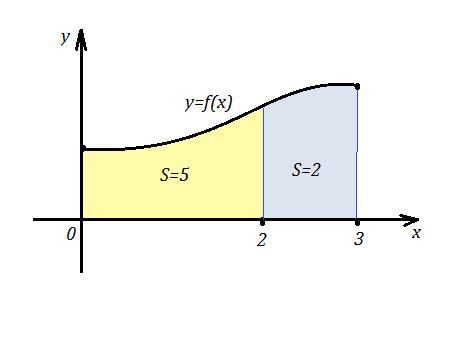
Определённый интеграл   $\int\limits^a_b\, f(x)\, dx$   численно равен площади криволинейной трапеции, ограниченной линиями  y=f(x) , y=0 , x=a , x=b .

На основании свойства аддитивности определённого интеграла имеем:

$\int\limits^3_0\, f(x)\, dx=\int\limits^2_0\, f(x)\, dx+\int\limits^3_2\, f(x)\, dx=5+2=7$

Answer 2

геометрич. смысл интеграла - площадь криволинейной трапеции, ограниченной прямыми х= 0, х=2, осью ох и графиком у=f(x), аналогично и для другого интеграла. Поэтому сумма интегралов равна интегралу от суммы т.е. 2+5=7, но при условии, что функция непрерывна и положительна.