Question

Помогите решить аналитическую геометрию, пожалуйста

Answer 1

1) Нормальный вектор заданной плоскости является направляющим вектором искомой прямой.

Получаем уравнение прямой через точку А(1; 2; 3) с направляющим вектором (3; -4; 1):

(x - 1)/3 = (y - 2)/(-4) = (z - 3)/1.

2) Находим точку пересечения прямых 4х + у - 13 = 0 и 8х - 3у -1 = 0.

Метод подстановки: у = 13 - 4х,     8х -3(13 - 4х) - 1 = 0,

8х - 39 + 12х - 1 =- 0,

20х = 40,

х = 40/20 = 2,   у = 13 - 4*2 = 5.   Точка А(2; 5).

Заданная параллельная прямая  имеет те же коэффициенты, что и прямая 3х + 4у - 5 = 0, только коэффициент С другой.

Подставим найденные координаты точки А(2; 5) в такое уравнение.

3*2 + 4*5 + С = 0, отсюда С = -26.

Ответ: уравнение 3х + 4у - 26 = 0.

3) По уравнениям заданных прямых имеем точки на них.

А(1; -2; -1) и В(0; 1; -2). Вектор АВ(-1; 3; -1).

Кроме того, имеем направляющий вектор прямых n = (3; -5; 4).

Нормальный вектор N искомой плоскости будет перпендикулярен векторам АВ и n. Найдём его как векторное произведение.

 i       j     k |      i      j

-1     3     -1 |    -1     3

3    -5      4 |    3    -5    = 12i - 3j  + 5k + 4j - 5i - 9k =

                                     = 7i + 1j - 4k.  Вектор N = (7; 1; -4).

 Для составления уравнения плоскости используем формулу:

nx(x - xA) + ny(y - yB) + nz(z - zC) = 0

Подставим данные и упростим выражение:

7 (x - 1)  + 1 (y - (-2)  + (-4)(z - (-1))  = 0

7x + y - 4z - 9 = 0 .

4) Дано уравнение 4x² + 9y² - 40x + 36y + 100 = 0.

Выделим полные квадраты.

 (4x² - 40x + 100) - 100 + (9y² + 36y + 36) - 36 + 100 = 0,

 4(x² - 10x + 25) + 9(y² + 4y + 4) - 36 = 0,

4(x - 5)² + 9(y + 2)²) = 36.

Разделим обе части на 36:

(4(x - 5)²/36) + (9(y + 2)²/36) = 1.

((x - 5)²/9) + ((y + 2)²/4) = 1.

Это уравнение эллипса. Приведём его к каноническому виду:

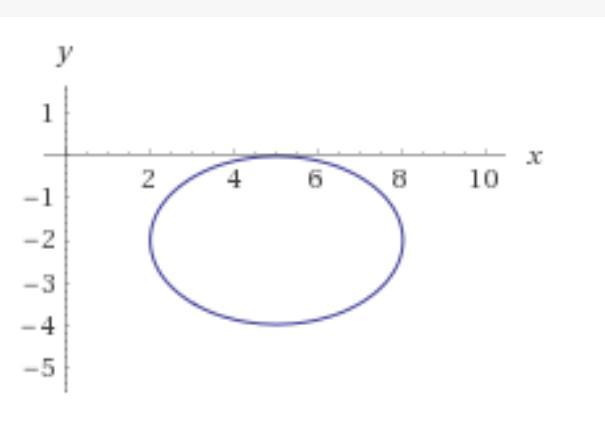
(x - 5)²/3²) + ((y + 2)²/2²) = 1.

Рисунок прилагается.