Предмет: Алгебра,
автор: Perfomance133
вычислить предел при х стремящимся к 2 (ВЫСШ.МАТ)
Приложения:
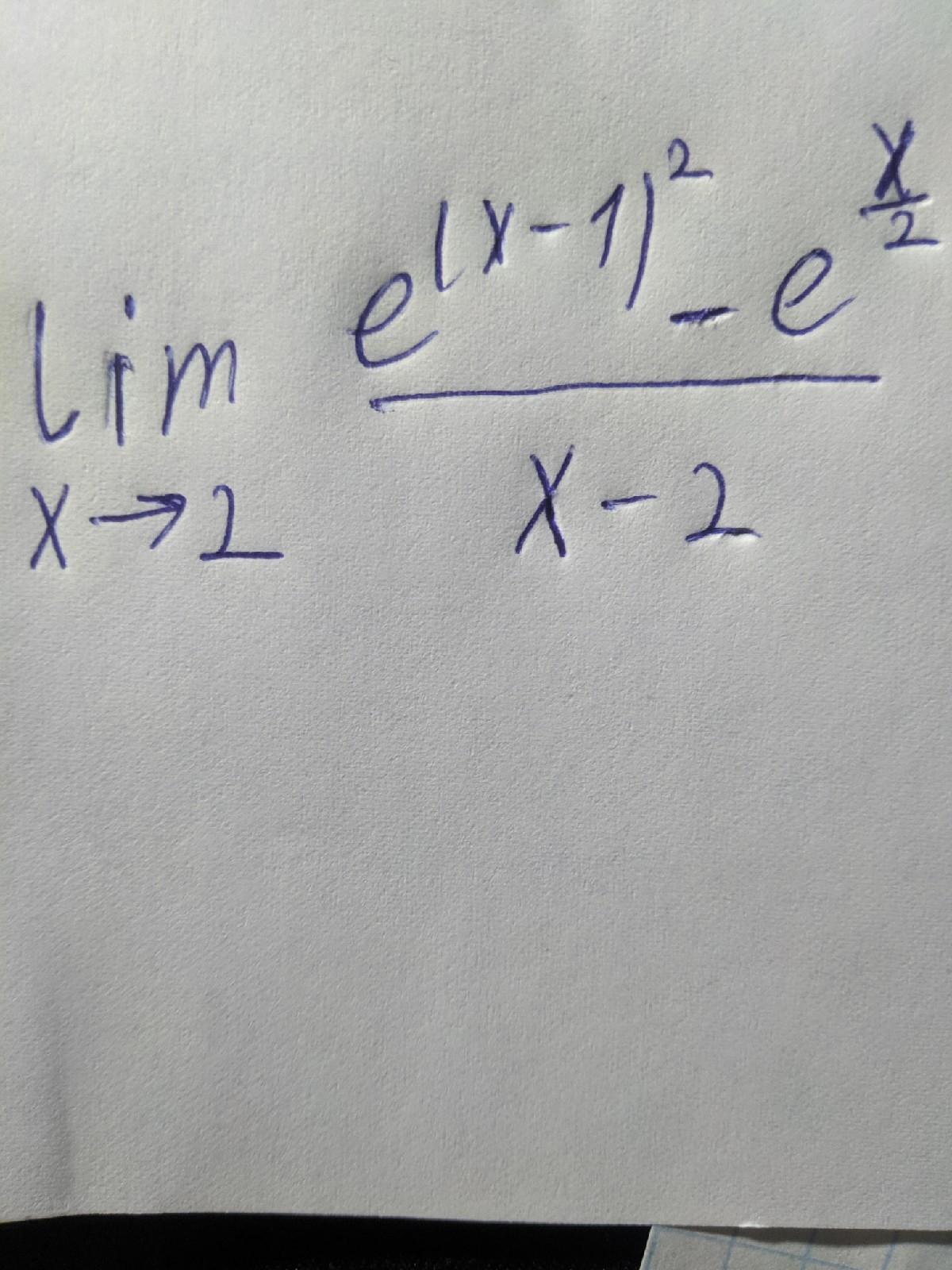
Ответы
Автор ответа:
0
я написал решение на листочке ===>>
Приложения:
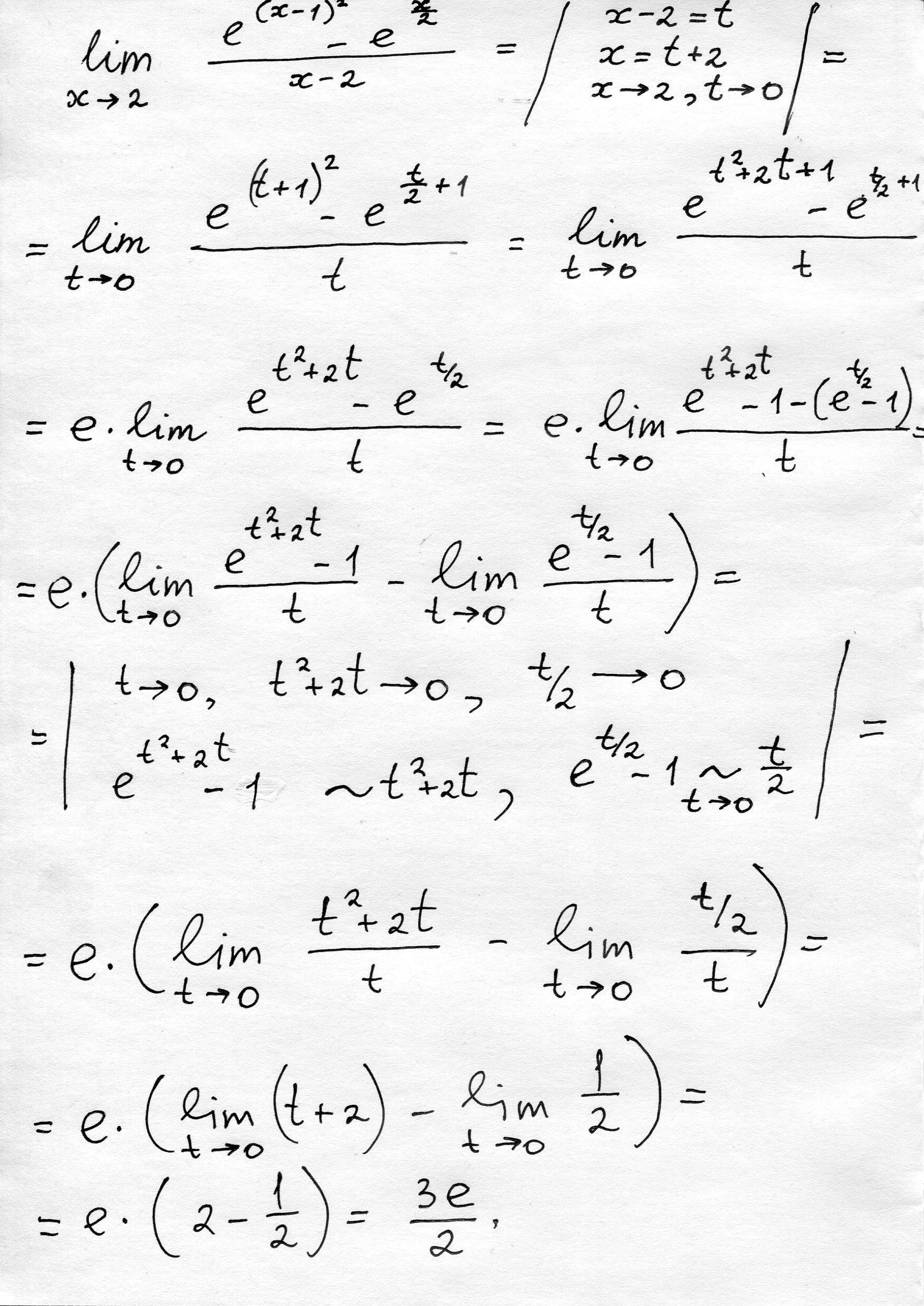
Автор ответа:
1
Похожие вопросы
Предмет: Алгебра,
автор: masha01021
Предмет: Английский язык,
автор: alyaxrq
Предмет: Английский язык,
автор: alyaxrq
Предмет: География,
автор: Аноним