Question

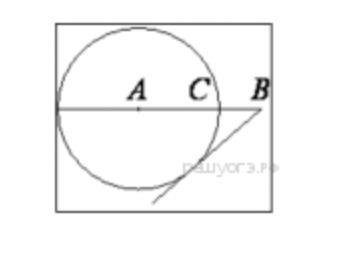
На от­рез­ке AB вы­бра­на точка C так, что AC= 68 и BC= 17. По­стро­е­на окруж­ность с цен­тром A, про­хо­дя­щая через C. Най­ди­те длину от­рез­ка ка­са­тель­ной, про­ведённой из точки B к этой окруж­но­сти.

Answer 1

Дано:

AC= 68  

BC= 17

BD - касательная (за точку D мы обозначили пересечение касательной с окружностью)

Найти: ВD

Решение:

AC=68 - радиус окружности

Достроим отрезок AD, соединяющий центр окружности с точкой D

Но AD - радиус окружности по построению, тогда AD= AC= 68

ΔABD - прямоугольный, т. к. ∠BAD = 90° (по свойству касательной)

По теореме Пифагора  ΔABD:

$c^{2} =a^{2}+b^{2}$

$BD=\sqrt{(AC+BC)^{2}-AD^{2}  } =\sqrt{(68+17)^{2} -68^{2} } =\sqrt{85^{2}-68^{2}  } =$$\sqrt{(85-68)*(85+68)}=\sqrt{17*153} =\sqrt{2601}=51$

Ответ: 51