Предмет: Геометрия,
автор: neznaika123363
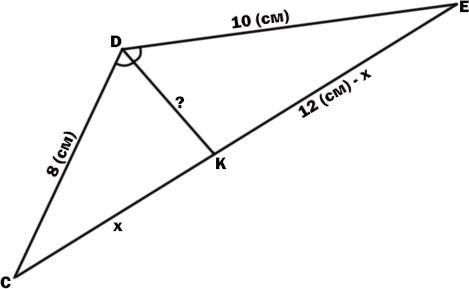
В треугольнике CDE известно что CD= 8 см,DE=10 см,CE= 12 см, DK биссектриса треугольника CDE. Найдите длину отрезка DK
Ответы
Автор ответа:
21
Дано :
ΔCDE.
СD = 8 см.
DE = 10 см.
СЕ = 12 см.
Отрезок DK - биссектриса ΔCDE.
Найти :
DK = ?
Решение :
Пусть СК = х, тогда КЕ = 12 (см) - х.
- Биссектриса угла треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.
Соответственно -
Подставим всё то, что нам известно и находим х -
- - -
cм
см.
- Квадрат длины биссектрисы угла треугольника равен произведению сторон, из которых выходит биссектриса, без произведения отрезков, на которая она делит третью сторону.
Запишем в виде формулы -
Осталось только подставить и подсчитать -
см.
Ответ :
(см).
Приложения:
Похожие вопросы
Предмет: Математика,
автор: koliesnikovrus
Предмет: Английский язык,
автор: bogdankrus267
Предмет: Английский язык,
автор: vexzt2009
Предмет: Алгебра,
автор: kiosse77