Предмет: Математика,
автор: odintsovayelizaveta
Исключить параметр t из параметрического уравнения траектории движения точки, получить уравнение в координатной форме
Приложения:
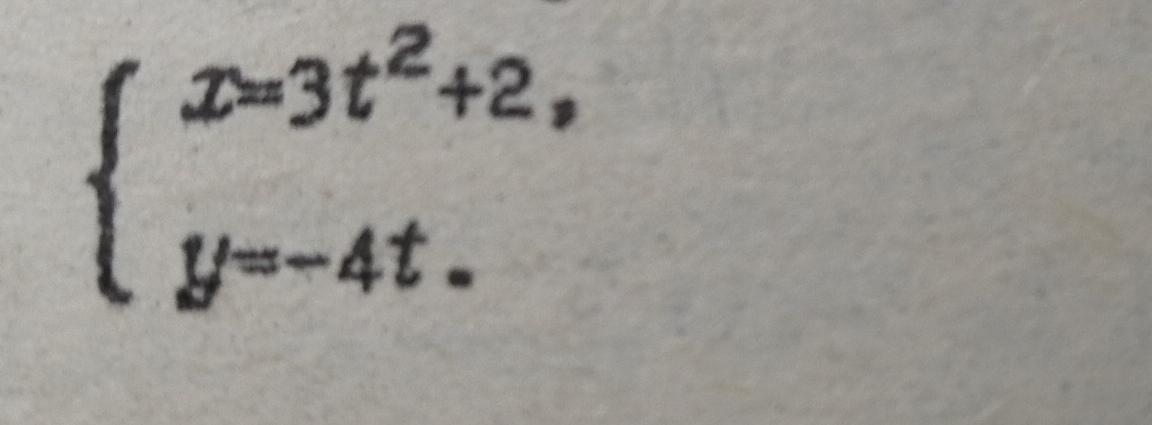
Ответы
Автор ответа:
0
Дано параметрическое уравнение:
x = 3t^2 + 2,
y = -4t.
Используем способ подстановки.
Из второго уравнения t = y/(-4) подставим в первое:
x = 3(y^2 / 16) + 2 = (3y^2 + 32) / 16.
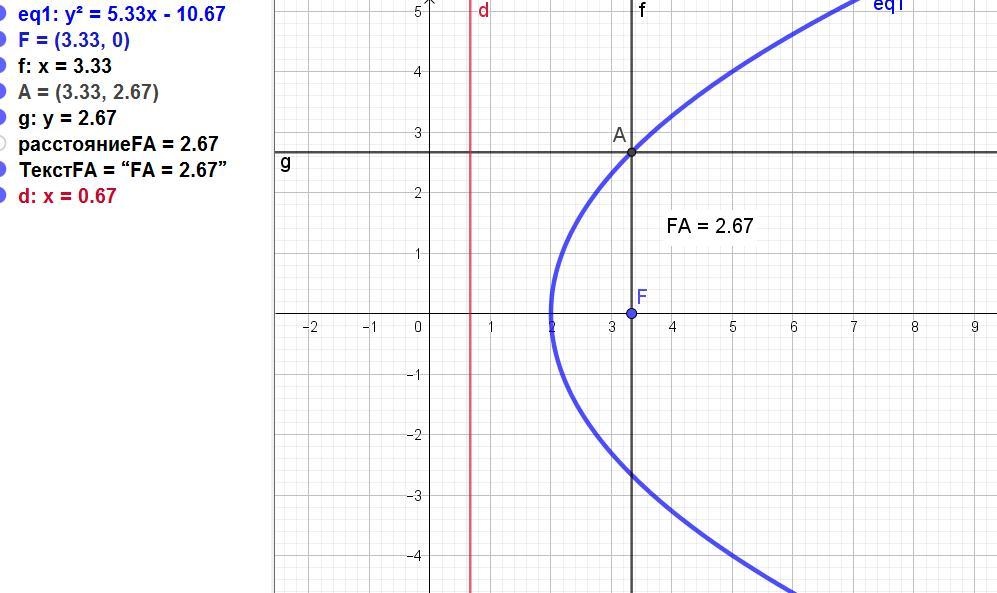
Получаем уравнение y^2 = (1/3)*(16x - 32).
Это уравнение параболы.
В каноническом виде её уравнение имеет вид:
y^2 = 2*(8/3)*(x - 2).
Из этого уравнения определяются параметры.
Ветви параболы направлены вправо, вершина расположена в точке (x0, y0), т.е. в точке (2;0).
Параметр р = (8/3).
Фокус в точке F = 2 + (p/2) = 2+(8/(3*2)) = 10/3.
Директриса d = 2 -(p/2) = 2 - (8/(3*2) = 2/3.
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: toha09821
Предмет: Математика,
автор: kacymovamilana
Предмет: Алгебра,
автор: toha09821
Предмет: Химия,
автор: алюмка4
Предмет: Математика,
автор: лев1979