Предмет: Алгебра,
автор: aid28
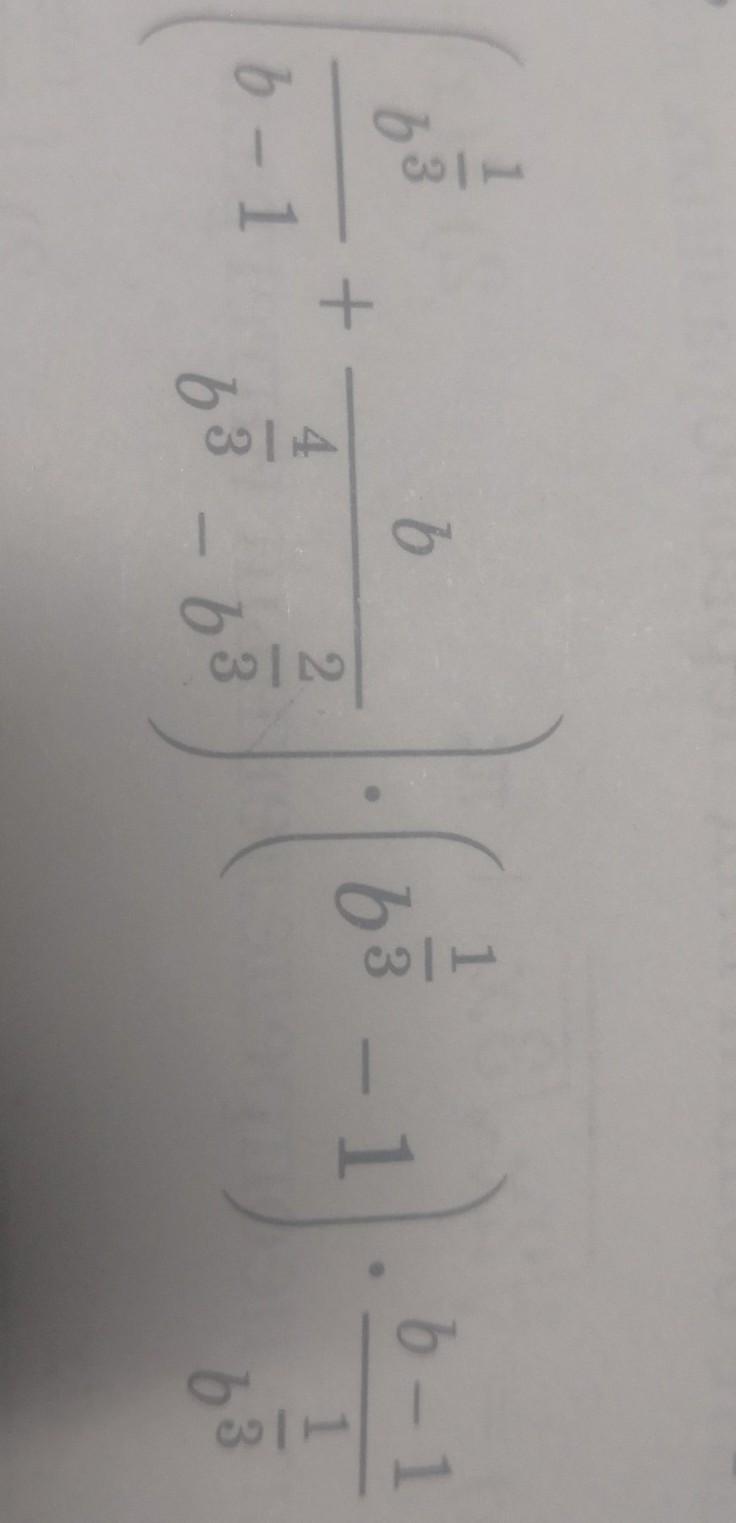
упростите выражение.
А)=b, B=-b, C=b 2/3-1, D=b^1/3-1
Приложения:
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Английский язык,
автор: dorv0521
Предмет: История,
автор: op20102006
Предмет: Математика,
автор: Kira1628
Предмет: Математика,
автор: rudveronika