Question

Помогите решить задачи даю 60 баллов спасибо за сотрудничество ✊
Номера: 2,4,5
Еще раз спасибо

Answer 1

Объяснение:

2.

$\left \{ {{\sqrt{\frac{x}{x-y}}=1 }} \atop {x^2+xy-4y^2=4}} \right. \ \ \ \ \ \left \{ {{(\sqrt{\frac{x}{x-y}})^2=1^2 }} \atop {x^2+xy-4y^2=4}} \right\ \ \ \ \ \left \{ {{{\frac{x}{x-y}}=1 }} \atop {x^2+xy-4y^2=4}} \right\ \ \ \ \left \{ {{x=x-y }} \atop {x^2+xy-4y^2=4}} \right\ \ \ \ \ \left \{ {{y=0 }} \atop {x^2=4}} \right\ \ \ \ \ \ \left \{ {{y=0} \atop {x_=-2\ \ \ \ x_2=2.}} \right.$

Ответ: (-2;0),  (2;0).

5.

$y=2\sqrt{x+1} \ \ \ \ \ x_0=3\ \ \ \ \ x=0\ \ \ \ \ S=?$

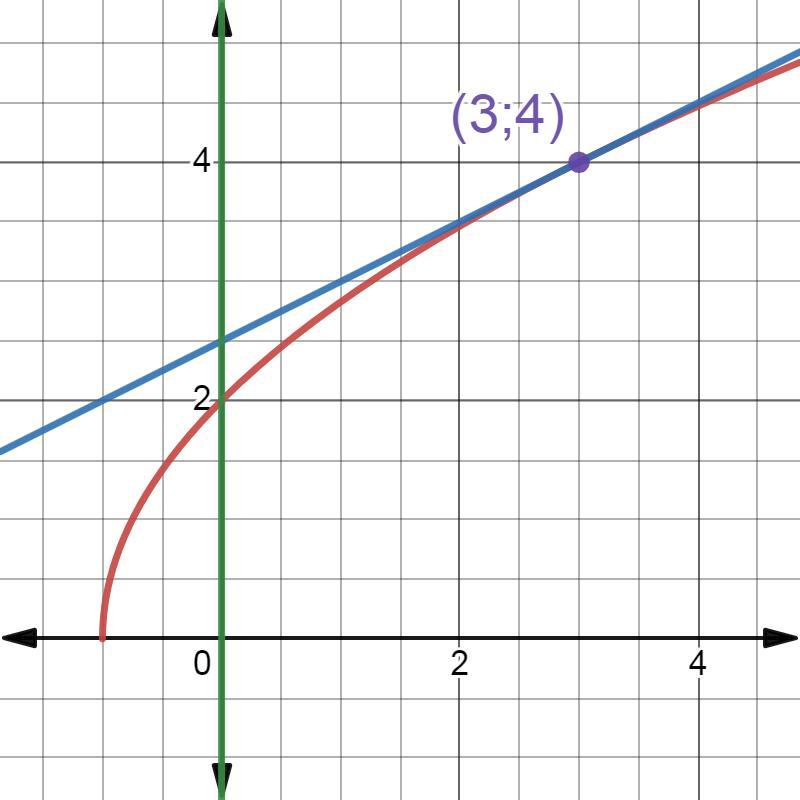
Найдём касательную линию.

$y_k=y(x_0)+y'(x_0)*(x-x_0)\\y(3)=2*\sqrt{3+1} =2*\sqrt{4} =2*2=4.\\y'(x_0)=(2\sqrt{x+1})'=2*((x+1)^\frac{1}{2})'=2*\frac{1}{2}*(\sqrt{x+1})^{-\frac{1}{2}}= \frac{1}{\sqrt{x+1} } .\\ y'(3)=\frac{1}{\sqrt{3+1} } =\frac{1}{\sqrt{4} } =\frac{1}{2}=0,5.\\ y_k=4+0,5*(x-3)=4+0,5x-1,5=0,5x+2,5.\\ y_k=0,5x+2,5.$

Найдём площадь фигуры.

$y=2\sqrt{x+1} \ \ \ \ \ y=0,5x+2,5\ \ \ \ x=0\ \ \ \ S=?\\2*\sqrt{x+1}=0,5x+2,5\ |*2\\ 4*\sqrt{x+1} =x+5\\(4*\sqrt{x+1})^2=(x+5)^2\\ 16*(x+1)=x^2+10x+25\\16x+16=x^2+10x+25\\x^2-6x+9=0\\(x-3)^2=0\\x-3=0\\x=3.\\S=\int\limits^3_0 {(0,5x+2,5-2*\sqrt{x+1} )} \, dx =\frac{x^2}{4}\ |_0^3+2,5x\ |_0^3- 2*\int\limits^3_0 {\sqrt{x+1}} \, dx=$

$\int\sqrt{x+1}dx=\boxed {u=x+1\ \ \ \ du=dx}=\int \sqrt{u} du =\int u^\frac{1}{2} du=\frac{2}{3} u^\frac{3}{2}=\frac{2}{3}(\sqrt{x+1})^3 .$

$=\frac{9}{4}+7,5-2*\frac{2}{3} *(\sqrt{x+1})^3\ |_0^3=2,25+7,5-\frac{4}{3}*(2^3 -1^3)=9,75- \frac{4*7}{3}=$

$=9\frac{3}{4} -\frac{28}{3}=\frac{39}{4}-\frac{28}{3}=\frac{39*3-28*4}{3*4} =\frac{117-112}{12}=\frac{5}{12}.$

Ответ: y=0,5x+2,5     S≈0,41667 кв. ед.