Question

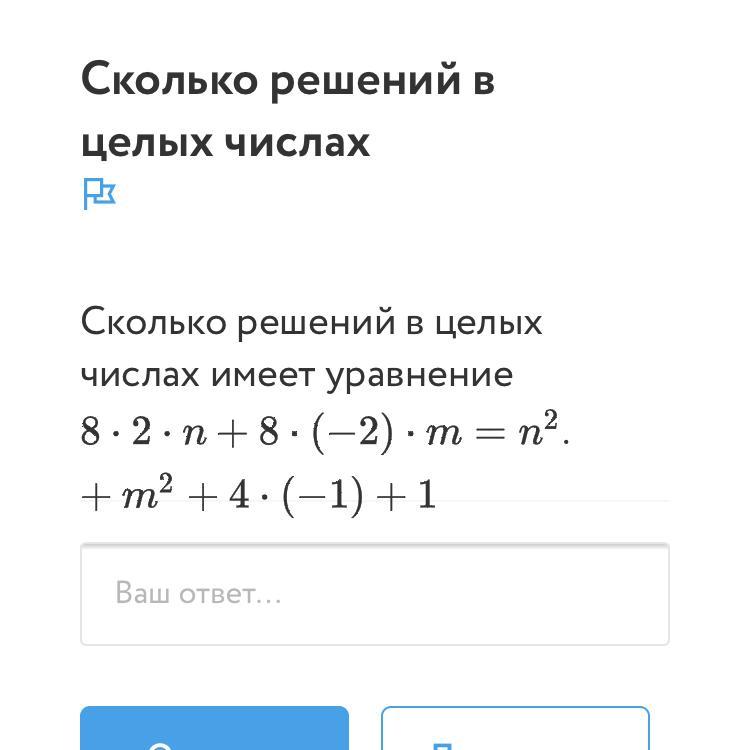
Сколько решений в целых числах имеет уравнение 8*2*n+8*(-2)*m=nквадрат+mквадрат+4*(-1)+1

Answer 1

Преобразуем наше уравнение:

$8\times2\times n+8\times(-2)\times m=n^2+m^2+4\times(-1)+1\\16n-16m=n^2+m^2-4+1\\n^2-16n+m^2+16m -3=0\\n^2-16n+64-64+m^2+16m+64-64 -3=0\\(n^2-16n+64)-64+(m^2+16m+64)-64 -3=0\\(n-8)^2-64+(m+8)^2-64-3=0\\(n-8)^2+(m+8)^2-131=0\\(n-8)^2+(m+8)^2=131$

Вот в таком виде смотрится уже лучше.

Заметим, что сумма квадратов двух чисел даёт нам "131".

Есть 2 пути:

1-ый путь (минимальная сложность). По условию корни уравнения целые числа, значит попытаемся подобрать корни нашего уравнения, используя таблицу квадратов (см приложение). Важно: числа мы берём сразу вместо скобок, наши переменные "m" и "n" нас пока не интересуют, их мы легко вычислим, если подберём значения скобок. Также не рассматриваем варианты, где одна из скобок больше 11-ти, т.к. 12 в квадрате это уже 144, что больше 131.

Перебрав все возможные варианты заметим, что число 131 невозможно представить в виде суммы квадратов двух целых чисел.

2-ой путь. Используем теорему о представлении простых чисел в виде суммы двух квадратов (Теорема Ферма — Эйлера). Она гласит, что любое простое число $p=4n+1$, где n — натуральное число, представимо в виде суммы квадратов двух натуральных чисел. В нашем случае p=131. Следовательно:

$131=4n+1\\130=4n\\n=32,5$

Число "n" не натуральное, а это значит, что 131 нельзя представить в виде суммы квадратов двух чисел.

Ответ: 0 решений.