Question

Есть прямоугольная доска размером 3х94 клеток. У Марины есть банка с синей краской. Она хочет покрасить 279 клеток доски так, чтобы из каждой клетки доски до любой другой можно было бы добраться, двигаясь только по синим клеткам (можно передвигаться только между клетками, имеющими общую сторону). Сколько способов покраски доски Марине не подойдут?

Answer 1

3·94 = 282

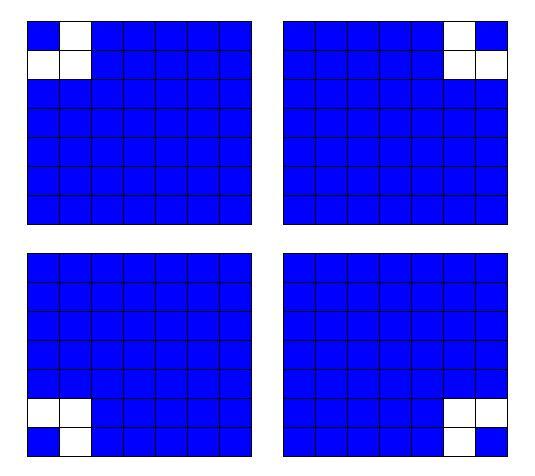
То есть всего 3 клетки не будут закрашены. Не подойдут те вариант покраски доски, при которых непокрашенные клетки будут "блокировать" покрашенные. Это возможно только в 4 случаях. Примеры "блокирования" на рисунке.