Предмет: Алгебра,
автор: SuperLisa
Найдите область определения функции
Приложения:
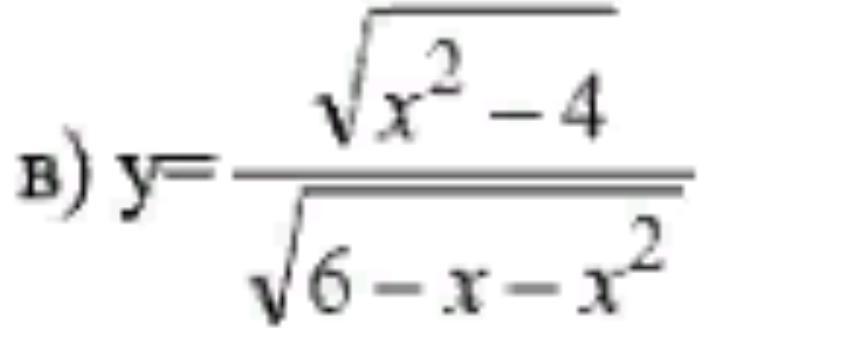
Ответы
Автор ответа:
1
Подкоренное выражение корня чётной степени должно быть неотрицательным, то есть ≥ 0 , но второй корень находится в знаменателе, а знаменатель не должен равняться нулю, так как на ноль делить нельзя. Следовательно подкоренное выражение корня, находящегося в знаменателе, должно быть строго больше нуля.
+ - +
1) ___________[-2]__________[2]_________
//////////////////////////// ////////////////////
+ - +
2)______(-3)_______________(2)_________
///////////////////////////////////
Ответ : x ∈ (-3 ; - 2]
Похожие вопросы
Предмет: Математика,
автор: avaskg6639
Предмет: Математика,
автор: nbhgyt83Artem
Предмет: Українська мова,
автор: ejhrhrfkerlidfy7yuye
Предмет: Алгебра,
автор: sashasakhar00
Предмет: Физика,
автор: vip1131