Question

Найти катеты прямоугольного треугольника,если гипотенуза равна 4 см,а косинус одного из углов 0,6.

Answer 1

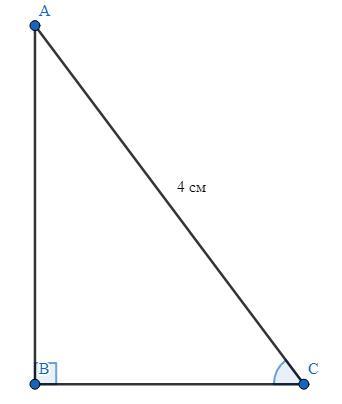
Дано :

ΔАВС - прямоугольный (∠В = 90°).

АС = 4 см, cos(∠С) = 0,6.

Найти :

АВ = ?, ВС = ?

Решение :

• Косинус острого угла прямоугольного треугольника - это отношение прилежащего катета к гипотенузе.

Следовательно, $cos(\angle C) = \frac{BC}{AC}$

$0,6 = \frac{BC}{4~cm} \\\\BC = 0,6*4~cm = 2,4~cm.$

• В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

Следовательно, AC² = AB² + BC² ⇒ AB² = AC² - BC² ⇒ АВ = $\sqrt{AC^{2} -BC^{2} } = \sqrt{4^{2}-2,4^{2} } = \sqrt{16-5,76} =\sqrt{10,24} = 3,2~cm.$

Ответ :

3,2 см, 2,4 см.

Answer 2

Ответ:

2,4 см и 3,2 см.

Объяснение:

ΔABC- прямоугольный ,

∠C=90°, ∠A=α, cos α=0,6.

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

$cos\alpha = \frac{AC}{AB} ;\\AC= AB*cos\alpha ;$

$AC= 4*0,6= 2,4$ см.

Найдем катет BC по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

$AB^{2} =AC^{2} +BC^{2} ;\\BC^{2} = AB^{2} - AC^{2} ;\\BC= \sqrt{AB^{2}-AC^{2} } ;\\BC= \sqrt{4^{2} -2,4^{2} } =\sqrt{16-5,76} =\sqrt{10,24} =3,2;$

BC= 3,2 см.