Предмет: Геометрия,
автор: Nektt
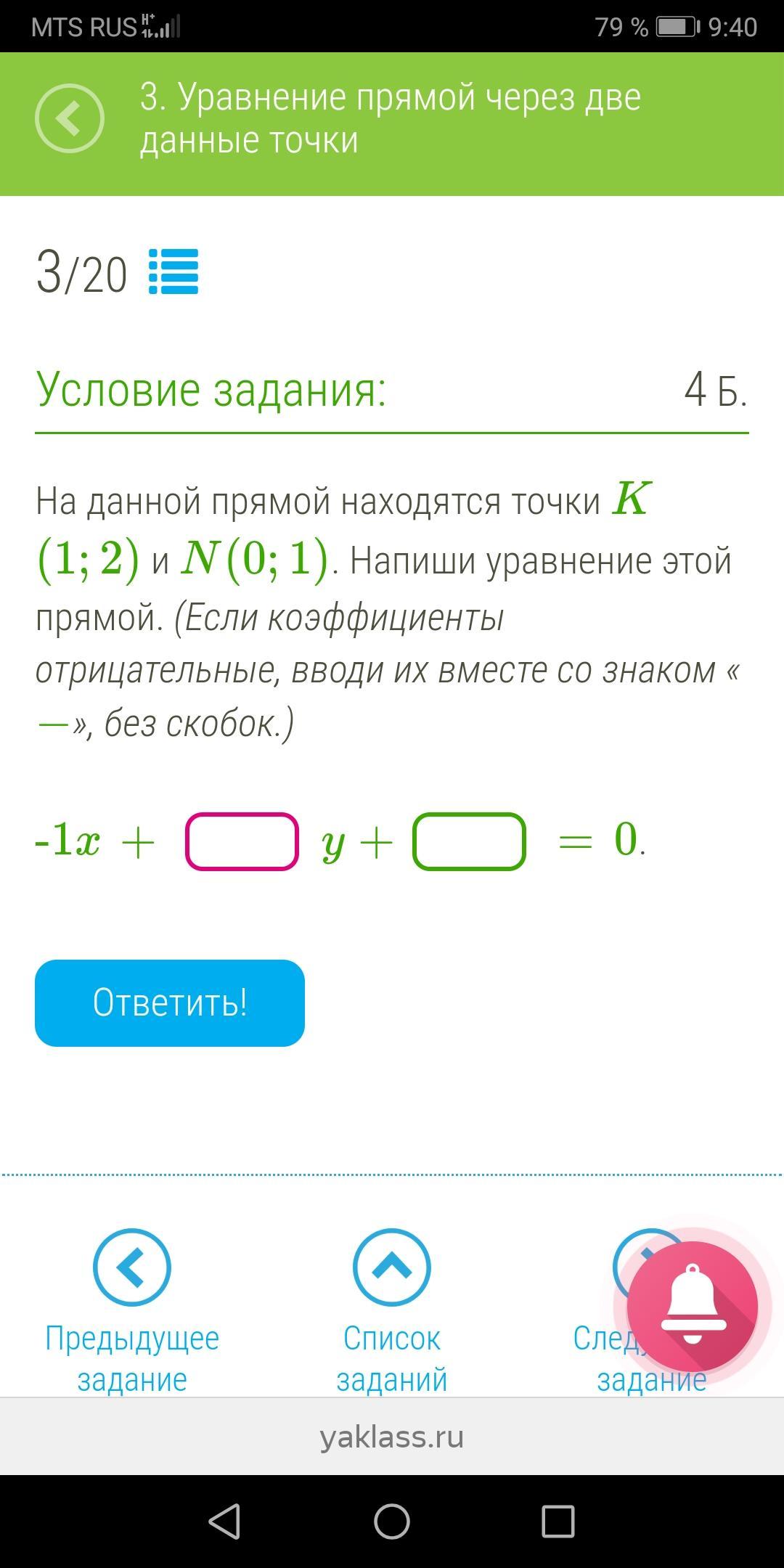
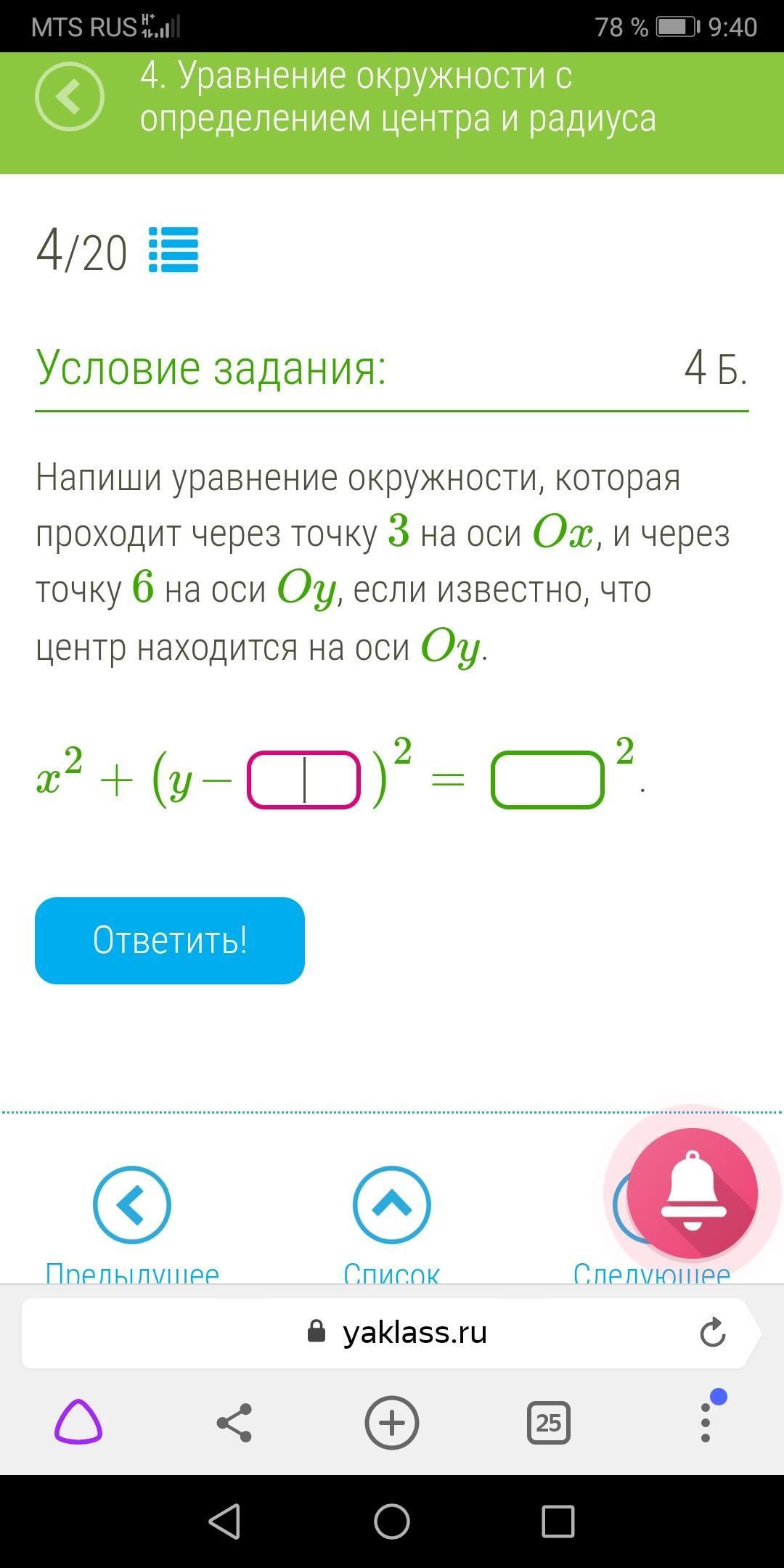
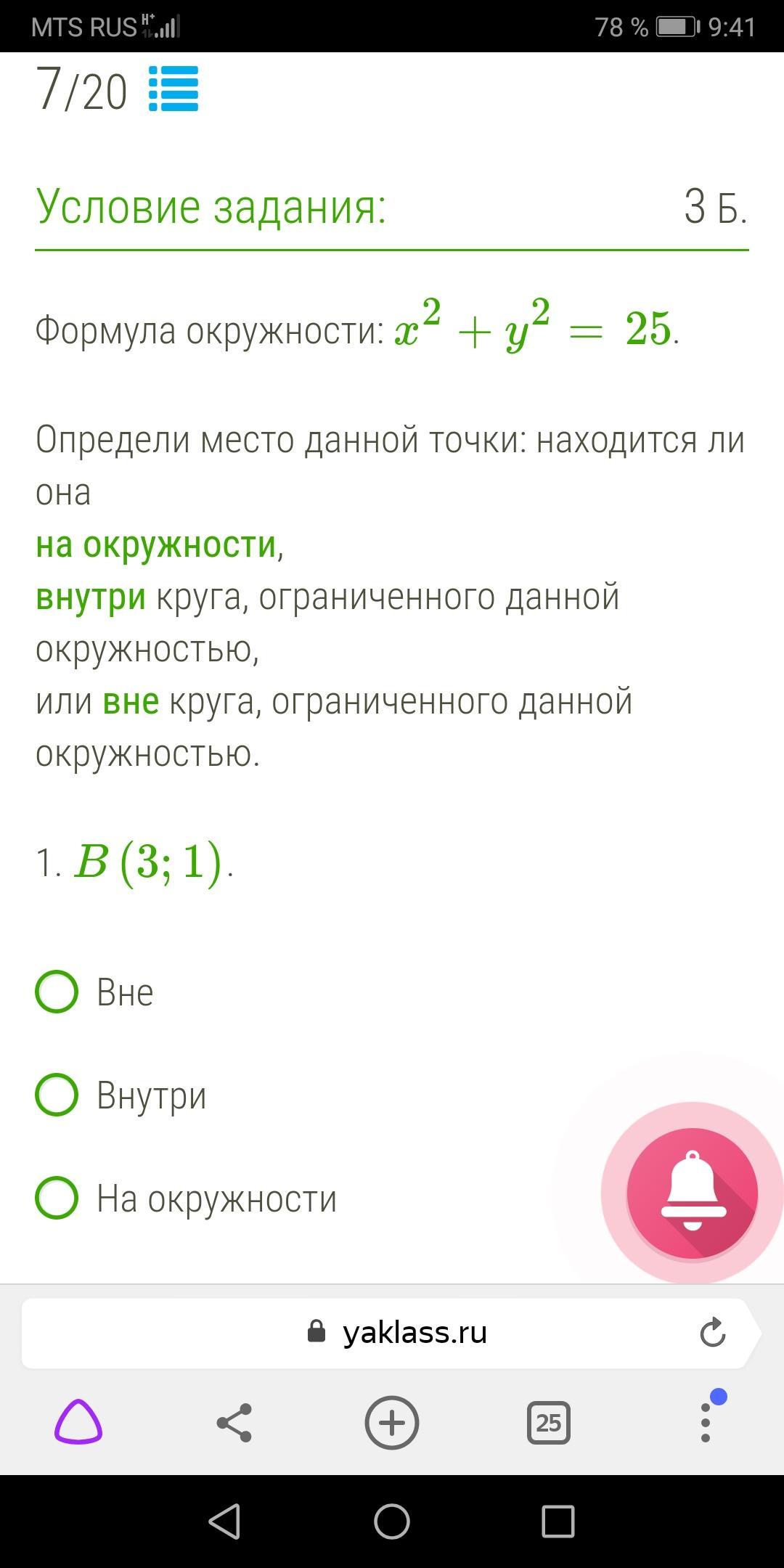
Помогите пожалуйста!!! Буду благодарен, даю максимальное кол-во баллов. Указывайте номер задания,он дан в фотографии
Приложения:


Ответы
Автор ответа:
0
точка находится внутри круга, ограниченного данной окружностью.
Nektt:
Спасибо
Похожие вопросы
Предмет: Физика,
автор: vityadxy13
Предмет: Математика,
автор: mm07b569
Предмет: История,
автор: romannikiforyk
Предмет: Обществознание,
автор: хзхзхз4
Предмет: Геометрия,
автор: Регина28138