Предмет: Математика,
автор: dermeco1
Математическое ожидание
Приложения:
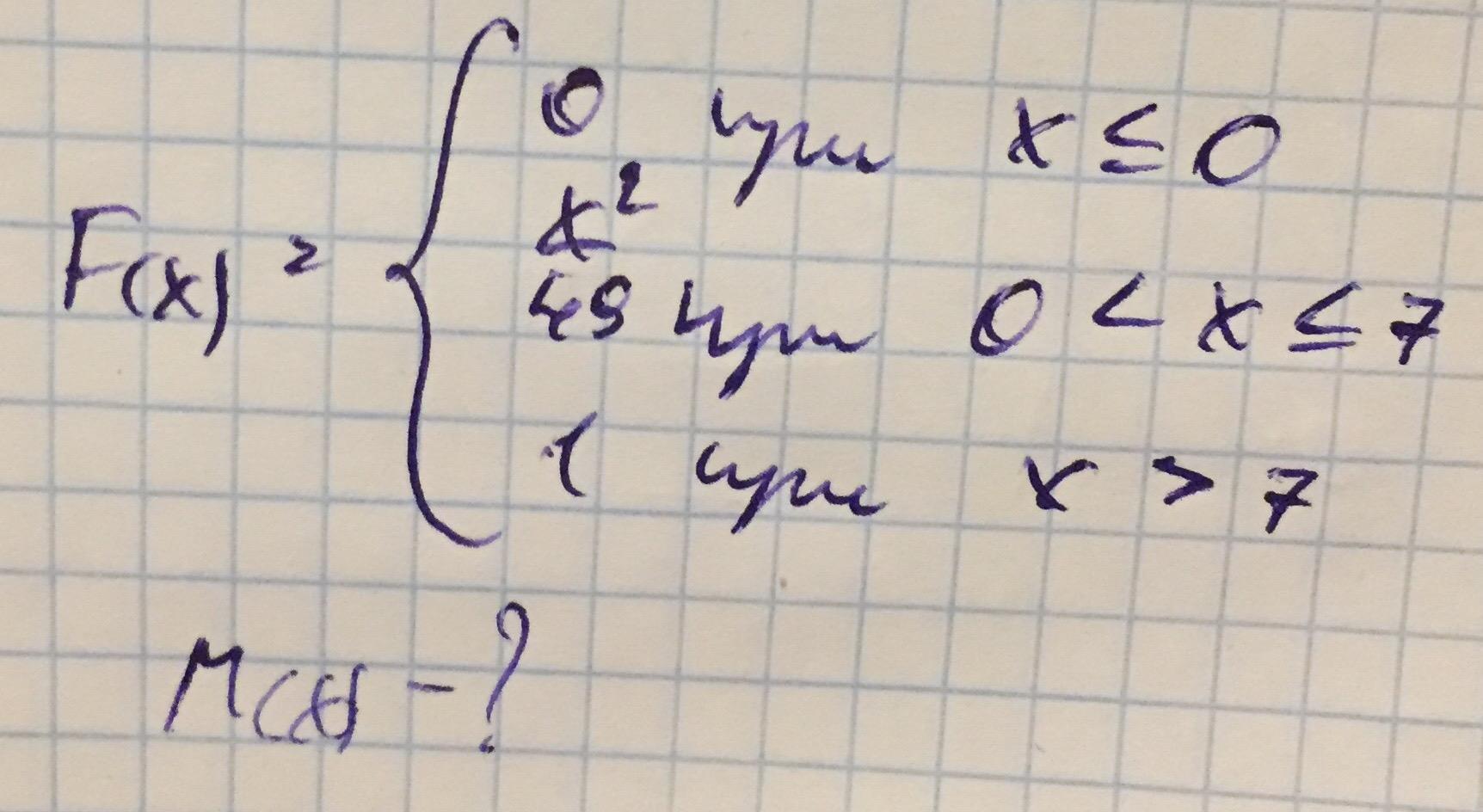
Ответы
Автор ответа:
0
Автор ответа:
0
Ответ: во вложении Пошаговое объяснение:
Приложения:
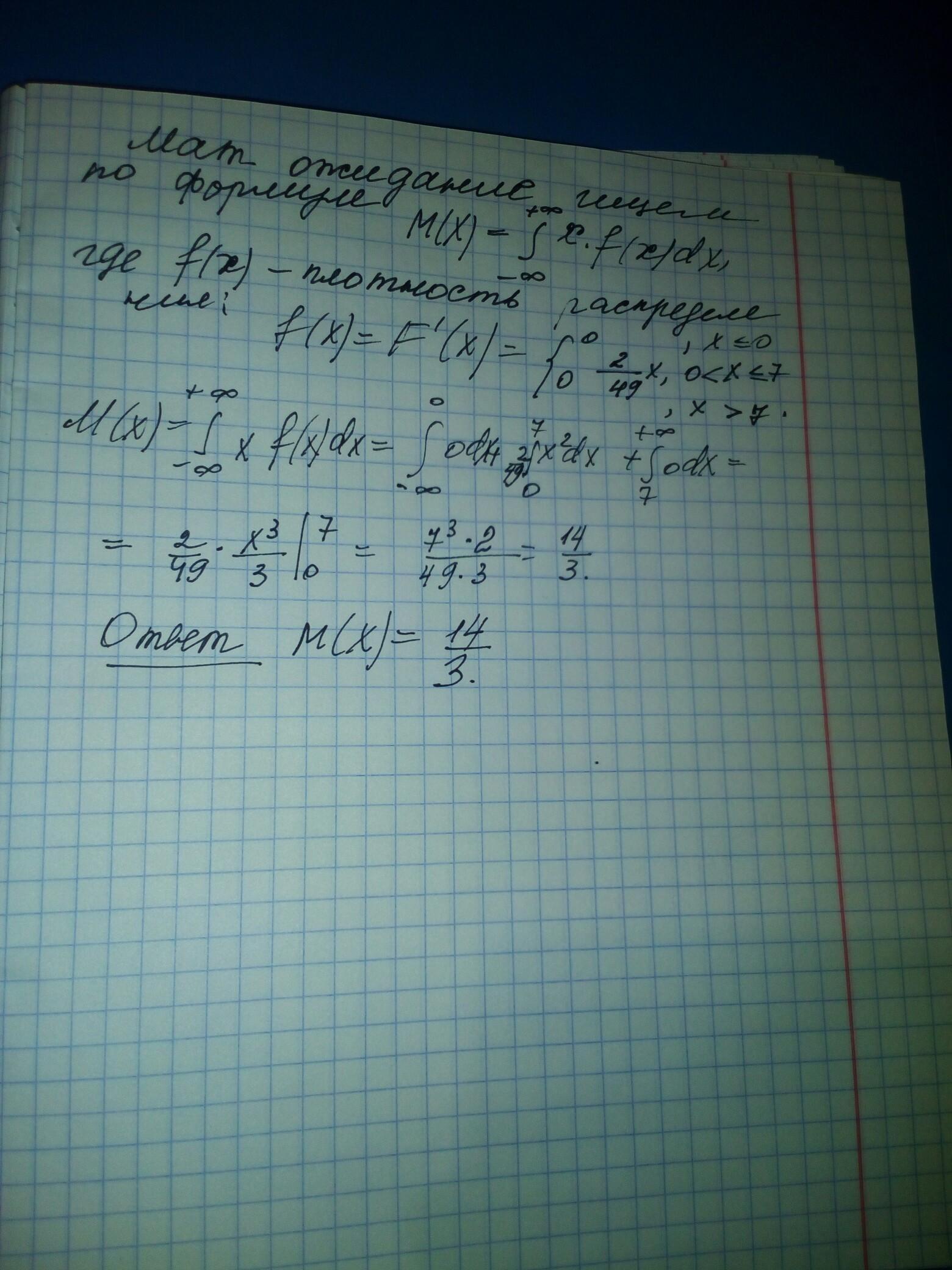
Похожие вопросы
Предмет: География,
автор: zapolskasasha882
Предмет: Биология,
автор: Yarik1234569734
Предмет: Информатика,
автор: salimamelikli
Предмет: Литература,
автор: yulia060183