Question

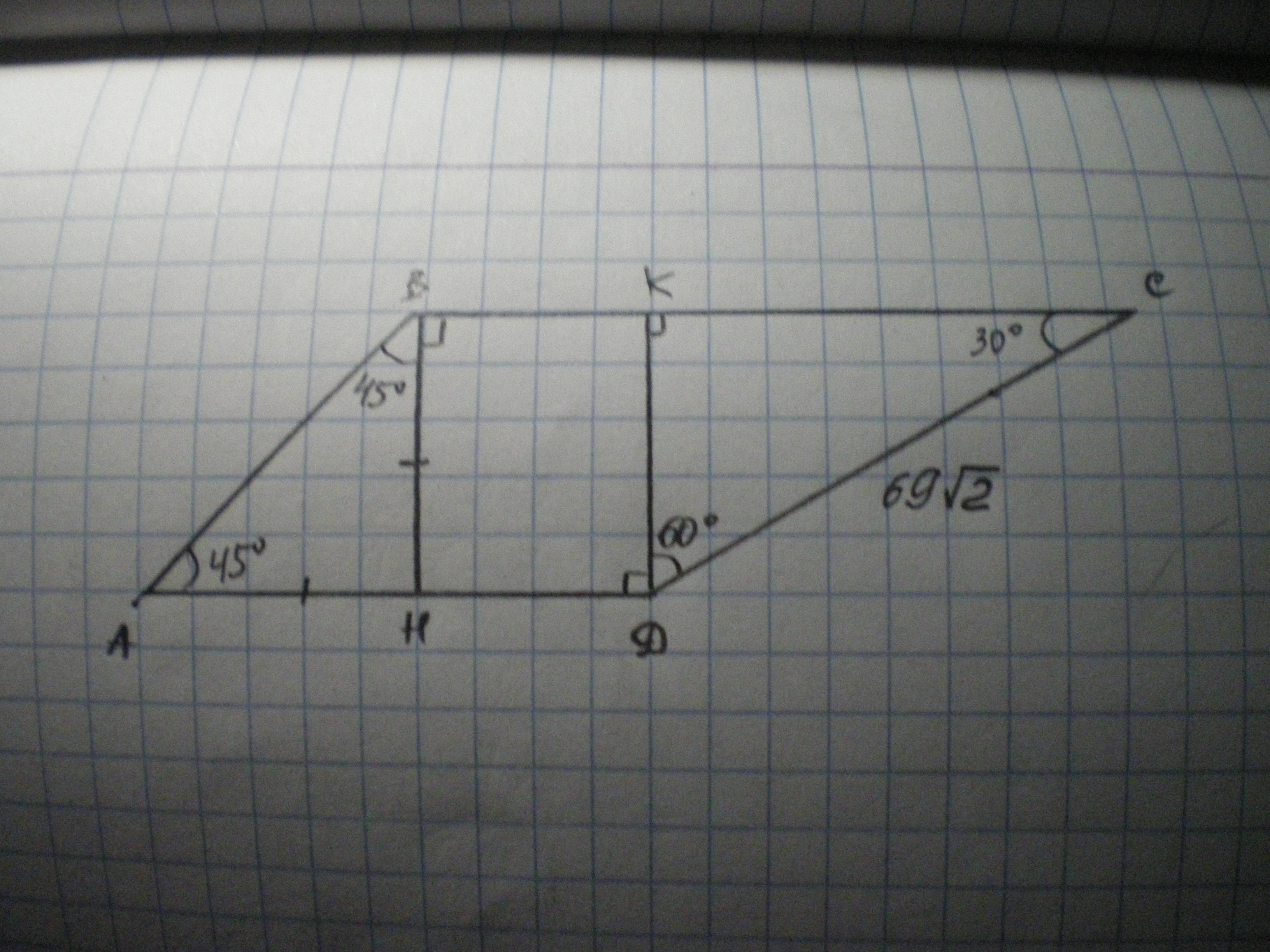
найдите боковую сторону AB трапеции ABCD, если угол ABC = 135 угол ADC = 150, CD = 69√2​

Answer 1

Ответ:

69 ед.изм.

Объяснение:

Дано: АВСD - трапеция, ∠АВС=135°, ∠ ADC=150°,  СD=69√2. Найти АВ.

Проведем высоты ВН и DК.

∠ КDC=150-90=60°;  ∠С=90-60=30°, тогда  по свойству катета, лежащего против угла 30°

DК=1/2*СD=(69√2):2=34,5√2.

ВН=DК=34,5√2.

∠АВН=135-90=45°, значит ∠А=90-45=45°, а АН=ВН=34,5√2.

По теореме Пифагора

АВ²=(34,5√2)²+(34,5√2)²=2380,5+2380,5=4761.

АВ=√4761=69 ед.изм.