Предмет: Алгебра,
автор: elizabetbess
Помогите пожалуста, нужно упросить выражение
Приложения:
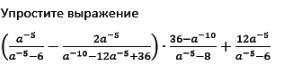
Ответы
Автор ответа:
1
elizabetbess:
Спасибо огромное, Вы очень помогли!
Всегда рада помочь )
Похожие вопросы
Предмет: Алгебра,
автор: meserakovagala821
Предмет: Химия,
автор: sasaaremkiv
Предмет: Алгебра,
автор: meserakovagala821
Предмет: Литература,
автор: sveta2022dasha