даю 100 баллов номер 5,6,7.
ПОДРОБНО СИСТЕМОЙ УРАВНЕНИЕЙ ЛИНЕЙНЫХ.
САМОЕ ГЛАВНОЕ ЭТО ПОДРОБНО У КОГО ПОДРОБНО ТОМУ ЛУЧШИЙ ОТВЕТ.

Ответы
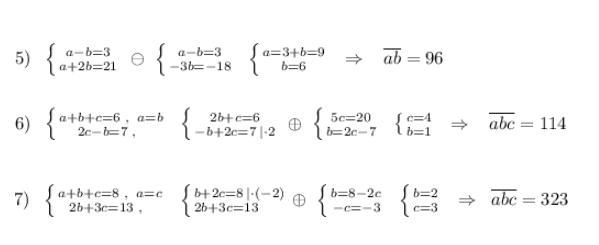
Пошаговое объяснение:
5. Пусть двузначное число ab , где а - число десятков , а b- число единиц.
По условию а= b+3 и a+2b=21 , получаем систему уравнений:
подставим значение а из первого уравнения во второе , получим
b+3+2b=21
3b=21-3
3b=18
b=18:3
b=6 , тогда
а=6+3=9
Искомое число 96
Проверка
9-6=3 - число десятков на 3 больше
9+2*6=9+12=21
21=21
6. Пусть искомое число abc, где а- число сотен, b-число десятков, с- число единиц. По условию число сотен равно числу десятков , т.е. a=b,
Сумма цифр равна 6 :
а+а+с=6
2а+с=6
и число десятков меньше удвоенного число единиц на 7
2с-а=7
Получаем систему уравнений :
подставим значение с из первого уравнения , во второе уравнение:
2*(6-2а)-а=7
12-4а-а=7
5а=5
а=5:5
а=1
с= 6-2*1=6-2=4
Искомое число 114
проверка
1+1+4=6 - сумма цифр равна 6 ( по условию)
2*4-1=7
8-1=7
7=7
7. Пусть искомое число abc, где а- число сотен, b- число десятков,
с- число единиц. По условию , число сотен равно числу единиц, значит
a=c, а сумма цифр равна 8. Получаем уравнение: a+b+a=8
2a+b=8 и
2*b+3*a=13
Получили систему уравнений :
Подставим значение b из первого уравнения во второе
2*(8-2а)+3а=13
16-4а+3а=13
16-13=4а-3а
а=3
b= 8-2*3=8-6=2
Искомое число будет 323
проверка
3+2+3=8
8=8
2*2+3*3=13
4+9=13
13=13