Question

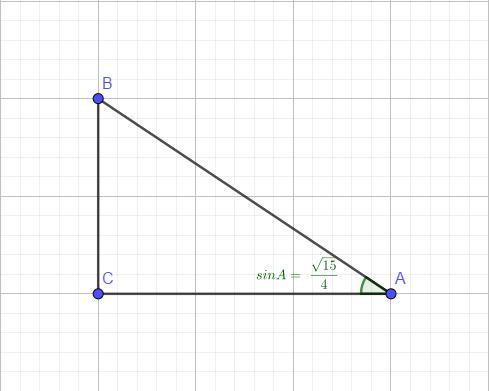
sin острого угла А треугольника АВС равен v15 : 4. Найдите cosA
v - корень​

Answer 1

Ответ:

0,25.

Объяснение:

$sin A = \frac{\sqrt{15} }{4}$

Воспользуемся основным тригонометрическим тождеством

$sin^{2} x+cos^{2} x=1;\\cos^{2} x=1- sin^{2} x;\\cos x =\pm\sqrt{1-sin^{2} x} ;$

Так как угол А острый , то косинус острого угла есть число положительное.

$cosA= \sqrt{1-sin^{2} A} ;\\cosA = \sqrt{1-(\frac{\sqrt{15} }{4})^{2} } = \sqrt{1-\frac{15}{16} } =\sqrt{\frac{1}{16} } =\frac{1}{4} = 0,25.$

Answer 2

Синус - есть отношение катета, противоположного искомому углу к гипотенузе.

Имеем:

$\displaystyle \frac{BC}{AB} =\frac{\sqrt{15} }{4}$

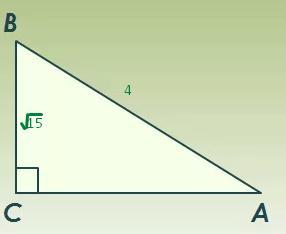
Построим треугольник, стороны которого примут нужные нам значения (смотри в приложении)

Косинус - есть отношение катета, прилежащего искомому углу к гипотенузе.

А именно:

$\displaystyle cosA=\frac{AC}{AB}$

По теореме Пифагора найдем недостающий катет.

c² = a² + b², где с - гипотенуза, а и b - катеты.

AB² = AC² + BC²

4² = AC² + (√15)²

16 = AC² + 15

AC² = 16 - 15

AC² = 1 (ед.)

AC = 1 (Сторона не может принять отрицательных значений)

Тогда:

$\displaystyle cosA=\frac{1}{4}=0.25$

Ответ: 0,25