Предмет: Математика,
автор: nikolairevens
Найти производную функции
СРОЧНО ПОЖАЛУЙСТА
Приложения:
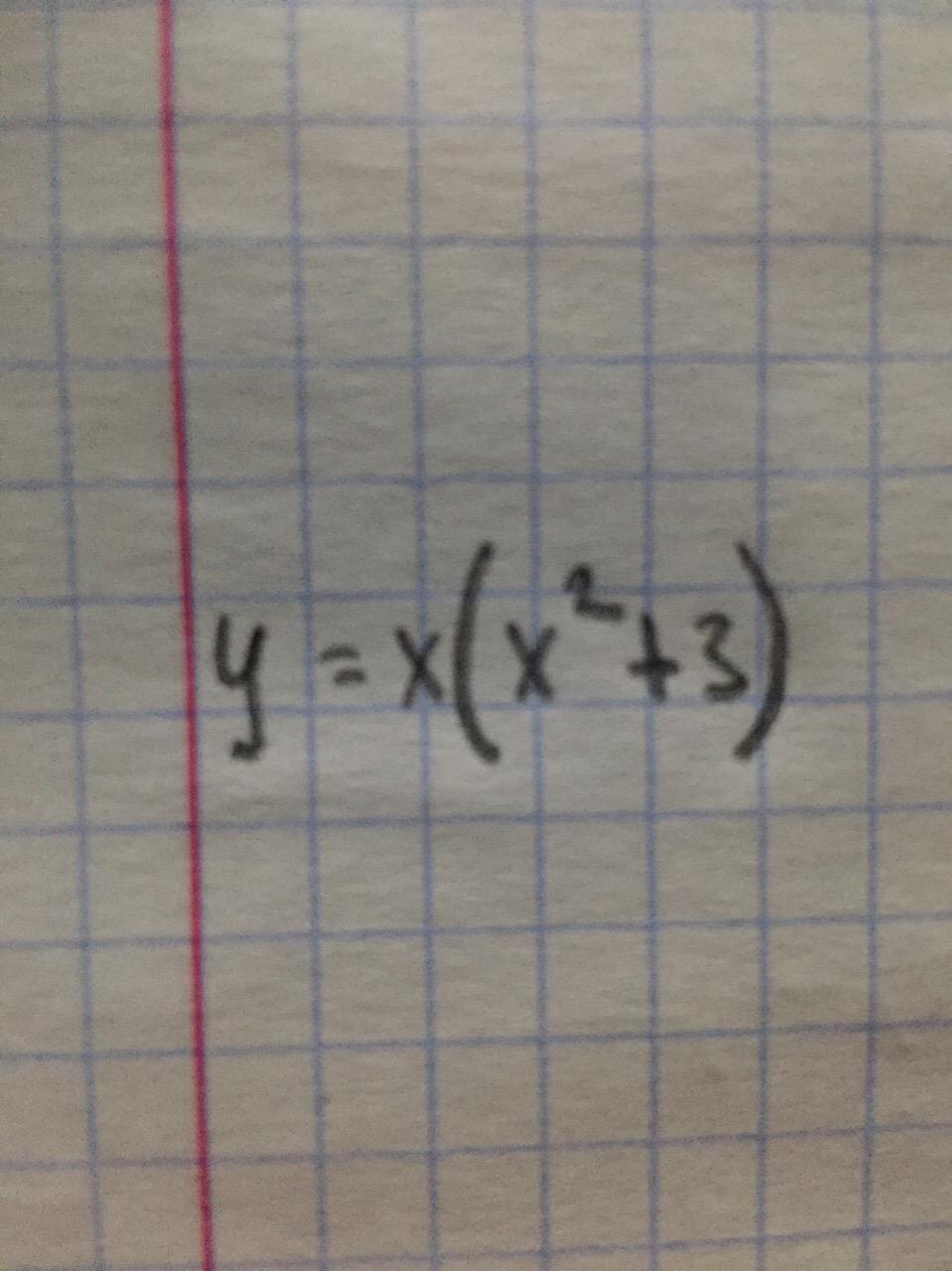
Ответы
Автор ответа:
1
y' = (x(x^2 + 3))'
Производная произведения вычисляется по формуле:
(ab)' = a'b + ab'
(x(x^2 + 3))' = (x)' * (x^2 + 3) + x * (x^2 + 3)'
Рассмотрим эти производные по отдельности
(x^n) = nx^(n - 1)
(x)' = (x^1)' = 1 * x^(1 - 1) = x^0 = 1
(x^2 + 3)'
Производная суммы равна сумме производных
(x^2 + 3)' = (x^2)' + (3)'
(x^2)' = 2x^(2 - 1) = 2x^1 = 2x
C' = 0, где C - константа, то есть, постоянное число
(3)' = 0
Запишем то, что у нас получилось
1 * (x^2 + 3) + x * (2x + 0) = (x^2 + 3) + x * 2x = (x^2 + 3) + 2x^2 = x^2 + 3 + 2x^2 = 2x^2 + x^2 + 3 = 3x^2 + 3 = 3 * (x^2 + 1)
Похожие вопросы
Предмет: Математика,
автор: object2164
Предмет: Математика,
автор: krupanastia03
Предмет: Литература,
автор: krekanna19
Предмет: История,
автор: dianausipova