Предмет: Алгебра,
автор: МаДиНаДАГ
Решите логарифмическое уравнение. Подробно пожалуйста
Приложения:
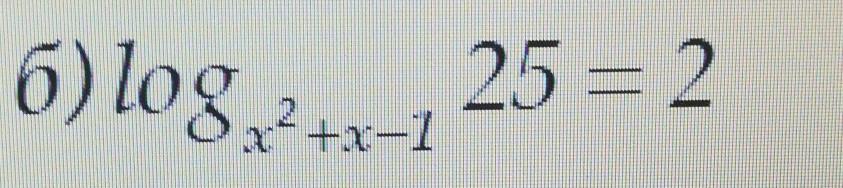
Ответы
Автор ответа:
0
Из определения логарифма
(x^2 + x - 1)^2 = 25
x^4 + 2x^3 - x^2 - 2x + 1 = 25
x^4 + 2x^3 - x^2 - 2x - 24 = 0
По теореме о том, что корни являются делителем свободного члена, имеем:
x = 1, -1, 2, -2, 3, -3, 4, -4, 6, -6, 8, -8, 12, -12, 24, -24
Если мы будем их проверять, то подойдут только x = 2 и x = -3
Nullpo201:
Тут вот такая штука, основание логарифма же >0 и не равен один, да?
А если (x²+x-1)² = 25, то x²+x-1 = ±5
Но -5 случай не рассматриваем, так как он меньше нуля
основание логарифма равно 5.
А корни у +5 автоматически проходят ОДЗ
смотрите ниже.
решение через модули
Я бы добавил к своему решению, но кто-то отметил его как нарушение и я не могу редактировать:
Смотри, на теореме про делители свободного члена мы определили корни, которые могут быть, но нужно проверить.
А чтобы проверить, можно из первого моего уравнения взять корень (учитывая, что корень это +-). Получатся уравнения x^2 + x - 6 = 0, что даст результат и x^2 + x - 4 = 0, что нам не даст нужных корней.
Смотри, на теореме про делители свободного члена мы определили корни, которые могут быть, но нужно проверить.
А чтобы проверить, можно из первого моего уравнения взять корень (учитывая, что корень это +-). Получатся уравнения x^2 + x - 6 = 0, что даст результат и x^2 + x - 4 = 0, что нам не даст нужных корней.
корень четной степени +- *
а стоп, второе уравнение x^2 + x + 4 = 0, но там дискриминант меньше нуля
Автор ответа:
0
Ответ: во вложении Объяснение:
Приложения:

Можно было и не делать проверку, если корни подставить в исходное уравнение, то x²+x-1 все равно будет равен 5, что удовлетворяет ОДЗ
Как по мне, всё супер
Решение как раз таки правильное, я не спорю
Никто не говорил, что оно не правильное
всем спасибо большое. Я создала ещё один вопрос, там 2 Уравнения, помогите пожалуйста
а я не вводил ОДЗ, с целью экономии времени). Но тогда проверка обязательна.
а проверка предусматривала работу с корнями, т.к. помимо того, что основание больше нуля, оно еще и не равно единице.
Просто 5 же он не равен одному, и уж точно больше нуля
Похожие вопросы
Предмет: История,
автор: footballtimipr
Предмет: География,
автор: Sashunya1311Sasha
Предмет: Алгебра,
автор: alinastelmah99
Предмет: Математика,
автор: ЭммаЯкубовская
Предмет: Алгебра,
автор: angel1260