Предмет: Алгебра,
автор: lidatupichenko
Помогите пожалуйста решить
Приложения:
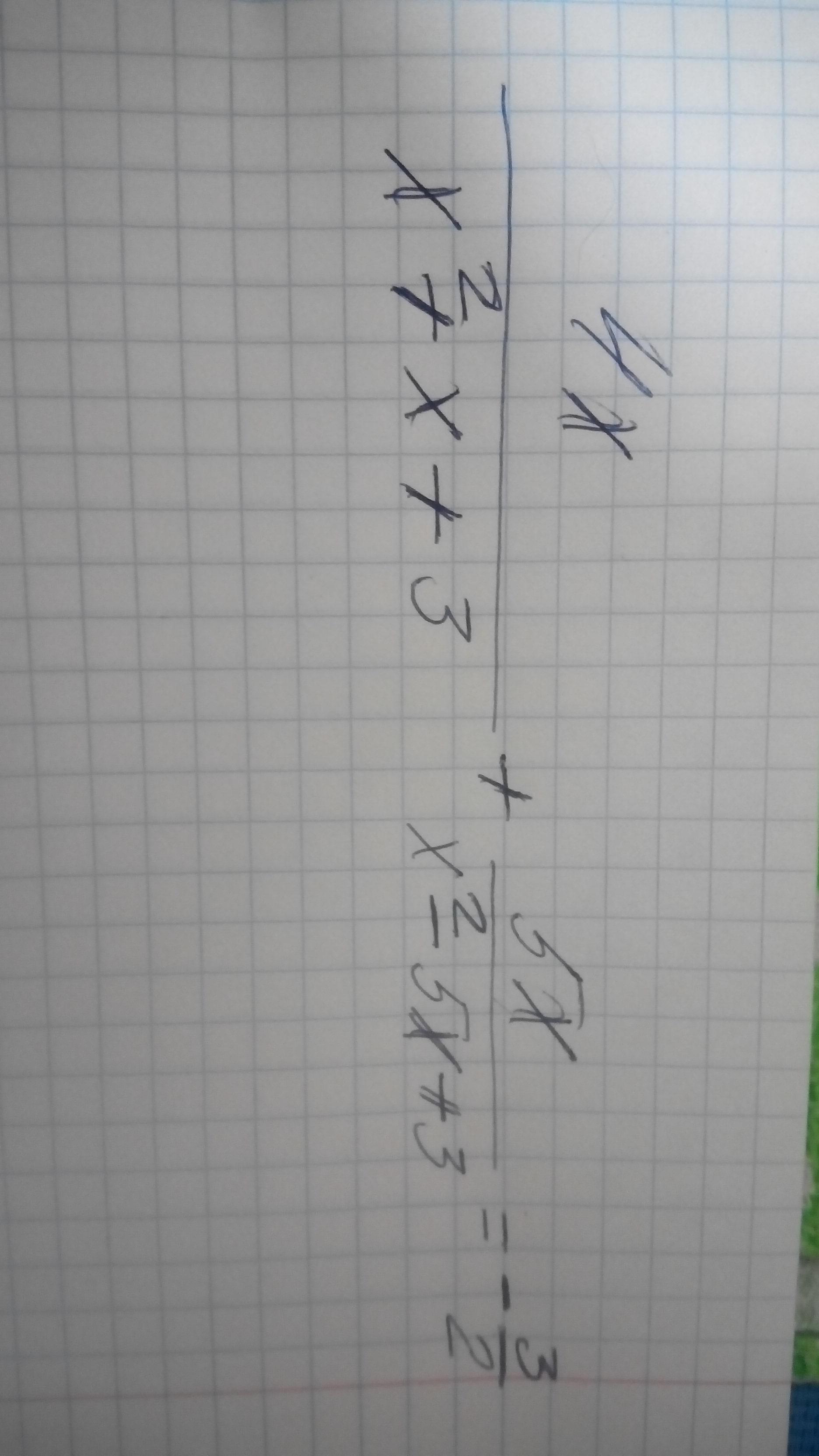
Ответы
Автор ответа:
0
Объяснение:
1) Проверим, что x=0 не является решением.
2) Разделим числитель и знаменатель каждой дроби на x, получим:
3) Введем замену переменной . Тогда:
4) Умножим обе части уравнения на
Отсюда
5) Вернемся к исходной переменной.
а) При t=-5:
x+3/x=-5
x²+5x+3=0
D=5²-4*3=13
x1,2=(-5±√13)/2
б) При t=3:
x+3/x=3
x²-3x+3=0
D=(-3)²-4*3=-3 - действительных решений нет.
Ответ: (-5±√13)/2.
Похожие вопросы
Предмет: Химия,
автор: krisnech2006
Предмет: Математика,
автор: pqndiss
Предмет: Окружающий мир,
автор: mksusha35
Предмет: Обществознание,
автор: оля1500