Предмет: Алгебра,
автор: MenycheCheam4elobek
решите неравенство
жпжпжпжпжпжпжпжпж
Приложения:
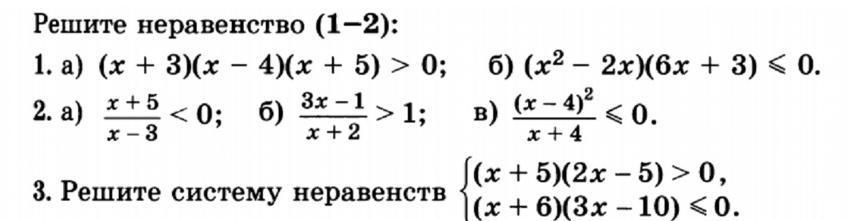
Namib:
Какое именно неравенство?
Ответы
Автор ответа:
1
Объяснение:
1.
а) точки x=-5;-3;4. Поэтому >0 при
x∈(-5;-3)∪(4;∞)
б) 6x(x-2)(x+0.5)≤0
точки x=-0.5;0;2. Поэтому ≤0 при
x∈(-∞;-0.5]∪[0;2]
2.
a) точки x=-5;3. Поэтому <0 при
x∈(-5;3)
б)
точки x=-2;2/3. Отсюда >0 при
x∈(-∞;-2)∪(2/3;∞]
в)
поэтому
спасибо
не полные ответы, учитель сразу спалит, можно их по очереде решение?
в комментарии
щас приведу вам пример
для каждого примера нужно ещё на оси x отметить указанные точки и "+" или "-" поставить для каждого промежутка, я к сожалению не имею возможности нарисовать (((
кроме этого больше не нужно никаких объяснений
щас вам покажу как мы на уроке решаем
Похожие вопросы
Предмет: Геометрия,
автор: Vladislad777
Предмет: Математика,
автор: staffa03
Предмет: Математика,
автор: irakabanova08
Предмет: Физика,
автор: Kolbyshevalana
Предмет: Математика,
автор: nargiza3333