Предмет: Алгебра,
автор: ilonaku
помогите решить хоть что-то
Приложения:
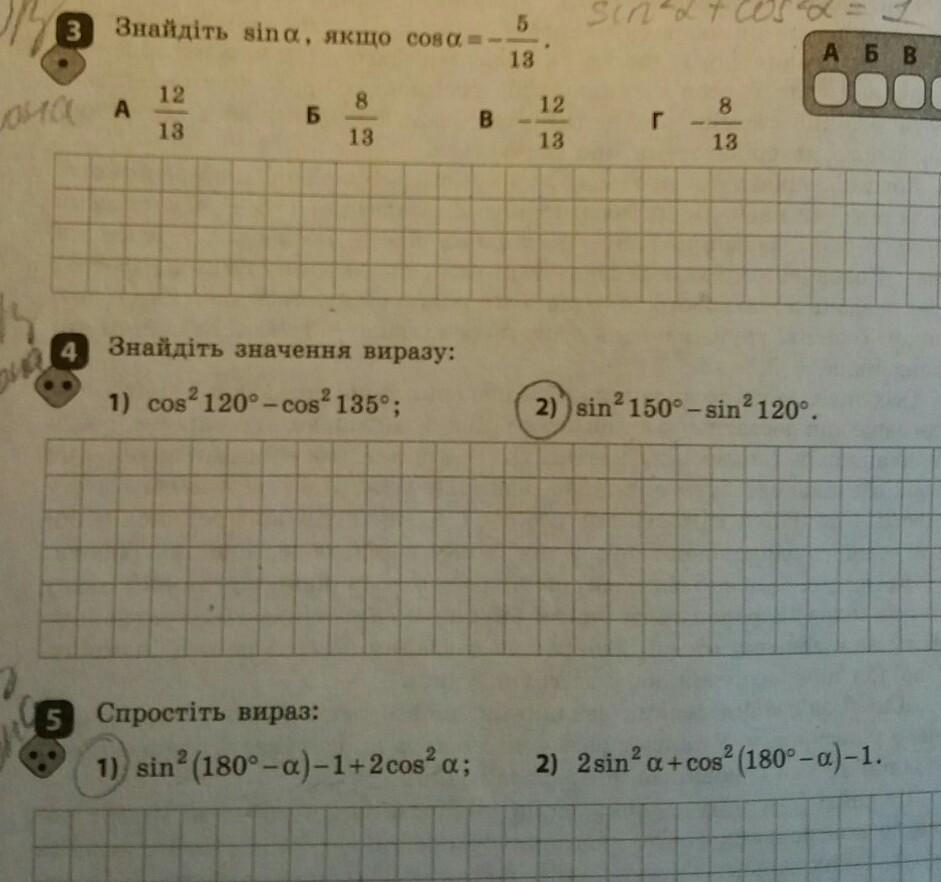
Universalka:
В третьем задании надо знать угол какой четверти задан. Если второй то ответ 12/13 , а если третьей то ответ - 12/13 .
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Физика,
автор: zylfat
Предмет: История,
автор: aliyaorazalina6633
Предмет: Биология,
автор: mcqonnaxeyy1392
Предмет: Обществознание,
автор: ghitrdg