Предмет: Математика,
автор: splash1396
Точка брошена наугад в круг x^2+y^2<=1. какова вероятность того, что расстояние от точки до центра превысит 0.5
Ответы
Автор ответа:
2
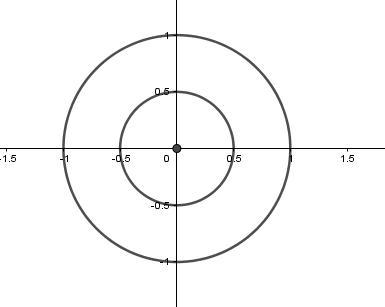
x² + y² ≤ 1 — окружность с центром (0;0) и радиусом R = 1, область которой лежит внутри окружности.
Расстояние от точки до центра окружности превысит 0.5, если эта точка не попадет в окружность с центром (0;0) и r = 0.5
Площадь большей окружности
Площадь меньшей окружности:
Разность
Вероятность того, что расстояние от точки до центра превысит 0,5, равна (по формуле геометрической вероятности):
Ответ: 0,75.
Приложения:
Похожие вопросы
Предмет: Химия,
автор: broandri930
Предмет: Английский язык,
автор: anastasia271034
Предмет: Физика,
автор: lololo7812
Предмет: Литература,
автор: Лёдвсердце
Предмет: Математика,
автор: Аноним