Предмет: Алгебра,
автор: mILEENNSSSSSS7
пределы нужно решить
Приложения:
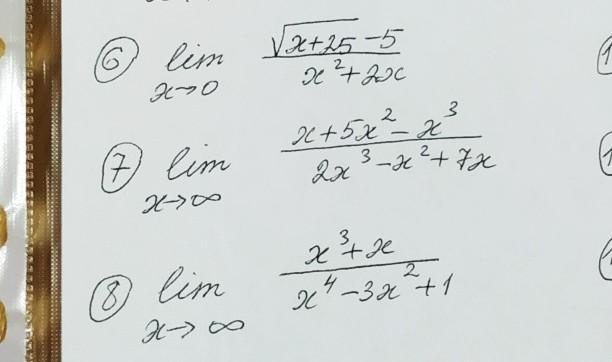
Ответы
Автор ответа:
1
Похожие вопросы