Предмет: Алгебра,
автор: sibirskiy17ynikum
Решите неравенство методом интервалов
Приложения:
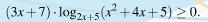
Ответы
Автор ответа:
0
x∈(-5/2;+∞)\{-2}
x∈(-∞;-7/3]∪[-2;+∞)
Наносим наше ограничение:
x∈(-5/2;-7/3]∪(-2;+∞)
Похожие вопросы
Предмет: Литература,
автор: volosmatvej19
Предмет: Биология,
автор: vovasidorenko234
Предмет: Қазақ тiлi,
автор: aminaabdibekova02
Предмет: Математика,
автор: пампасс
Предмет: Физика,
автор: klukashova98