Предмет: Алгебра,
автор: Bui
Найдите предел


Приложения:
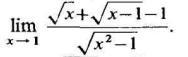
Ответы
Автор ответа:
1
Bui:
Что в первом действии произошло?
Похожие вопросы
Предмет: Алгебра,
автор: Defensivofvik
Предмет: География,
автор: hackkotik228
Предмет: География,
автор: mykolaiv689
Предмет: Математика,
автор: kuzjlad
Предмет: История,
автор: Liza1357911