Предмет: Математика,
автор: VladislavLebronov
Помогите пожалуйста, мне срочно нужно, а не знаю как его решать, помогите пожалуйста, любой пример
Приложения:
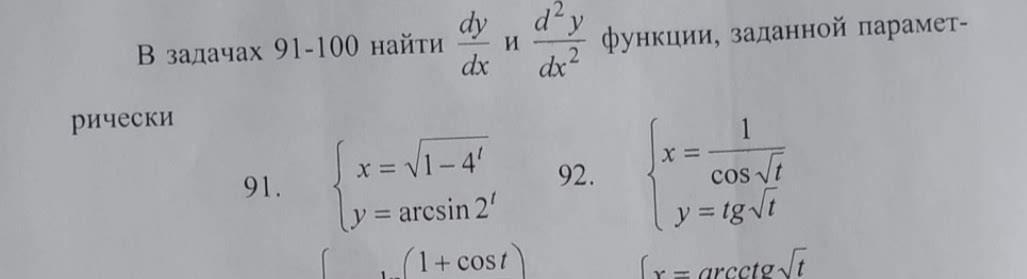
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Геометрия,
автор: playertimofey
Предмет: Русский язык,
автор: markal09
Предмет: Английский язык,
автор: aleksandrakaraseva44
Предмет: Математика,
автор: aika9626
Предмет: Химия,
автор: Magameed