Решить систему линейных алгебраических уравнений методом Гаусса, или доказать что система не имеет решений
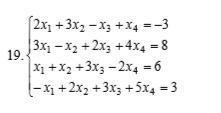
Ответы
Пошаговое объяснение:
Переведем СЛУ в матричный вид:
(2 3 -1 1 | -3)
(3 -1 2 4 | 8)
(1 1 3 -2 | 6)
(-1 2 3 5 | 3)
1-я строка:
2/2=1; 3/2=1,5; -1/2=-0,5; 1/2=0,5; -3/2=-1,5
(1 1,5 -0,5 0,5 | -1,5)
2-я строка:
3-1•3=0; -1-1,5•3=-5,5; 2-(-0,5)•3=3,5; 4-0,5•3=2,5; 8-(-1,5)•3=12,5
(0 -5,5 3,5 2,5 | 12,5)
3-я строка:
1-1•1=0; 1-1,5•1=-0,5; 3-(-0,5)•1=3,5; -2-0,5•1=-2,5; 6-(-1,5)•1=7,5
(0 -0,5 3,5 -2,5 | 7,5)
4-я строка:
-1+1•1=0; 2+1,5•1=3,5; 3+(-0,5)•1=2,5; 5+0,5•1=5,5; 3+(-1,5)•1=1,5
(0 3,5 2,5 5,5 | 1,5)
Общий вид:
( 1 1,5 -0,5 0,5 | -1,5)
( 0 -5,5 3,5 2,5 | 12,5)
( 0 -0,5 3,5 -2,5 | 7,5)
( 0 3,5 2,5 5,5 | 1,5)
2-я строка:
0/(-5,5)=0; -5,5/(-5,5)=1; 3,5/(-5,5)=-7/11; 2,5/(-5,5)=-5/11; 12,5/(-5,5)=-25/11
(0 1 -7/11 -5/11 | -25/11)
1-я строка:
1-0•1,5=1; 1,5-1•1,5=0; -0,5-(-7/11)•1,5=-5,5/11 +10,5/11=5/11; 0,5-(-5/11)•1,5=5,5/11 +7,5/11=13/11; -1,5-(-25/11)•1,5=-16,5/11 +37,5/11=21/11
(1 0 5/11 13/11 | 21/11)
3-я строка:
0+0•0,5=0; -0,5+1•0,5=0; 3,5+(-7/11)•0,5=38,5/11 -3,5/11=35/11; -2,5+(-5/11)•0,5=-27,5/11 -2,5/11=-30/11; 7,5+(-25/11)•0,5=82,5/11 -12,5/11=70/11
4-я строка:
0-0•3,5=0; 3,5-1•3,5=0; 2,5-(-7/11)•3,5=27,5/11 +24,5/11=52/11; 5,5-(-5/11)•3,5=60,5/11 +17,5/11=78/11; 1,5-(-25/11)•3,5=16,5/11 +87,5/11=104/11
Общий вид:
( 1 0 5/11 13/11 | 21/11)
( 0 1 -7/11 -5/11 | -25/11)
( 0 0 35/11 -30/11 | 70/11)
( 0 0 52/11 78/11 | 104/11)
3-я строка:
0/(35/11)=0; 0/(35/11)=0; (35/11)/(35/11)=1; (-30/11)/(35/11)=-6/7; (70/11)/(35/11)=2
( 0 0 1 -6/7 | 2)
1-я строка:
1-0•5/11=1; 0-0•5/11=0; 5/11 -1•5/11=0; 13/11 -(-6/7)•5/11=91/77 +30/77=121/77=11/7; 21/11 -2•5/11=1
( 1 0 0 11/7 | 1)
2-я строка:
0+0•7/11=0; 1+0•7/11=1; -7/11 +1•7/11=0; -5/11 +(-6/7)•7/11=-1; -25/11 +2•7/11=-1
( 0 1 0 -1 | -1)
4-я строка:
0-0•52/11=0; 0-0•52/11=0; 52/11 -1•52/11=0; 78/11 -(-6/7)•52/11=546/77 +312/77=858/77=78/7; 104/11 -2•52/11=0
(0 0 0 78/7 | 0)
Общий вид:
( 1 0 0 11/7 | 1)
( 0 1 0 -1 | -1)
( 0 0 1 -6/7 | 2)
( 0 0 0 78/7 | 0)
4-я строка:
0/(78/7)=0; 0/(78/7)=0; 0/(78/7)=0; (78/7)/(78/7)=1; 0/(78/7)=0
( 0 0 0 1 | 0)
1-я строка:
1-0•11/7=1; 0-0•11/7=0; 0-0•11/7=0;
11/7 -1•11/7=0; 1-0•11/7=1
( 1 0 0 0 | 1)
2-я строка:
0+0•1=0; 1+0•1=1; 0+0•1=0; -1+1•1=0; -1+0•1=-1
( 0 1 0 0 | -1)
3-я строка:
0+0•6/7=0; 0+0•6/7=0; 1+0•6/7=1; -6/7 +1•6/7=0; 2+0•6/7=2
( 0 0 1 0 | 2)
Общий вид:
( 1 0 0 0 | 1)
( 0 1 0 0 | -1)
( 0 0 1 0 | 2)
( 0 0 0 1 | 0)
Ответ: х1=1; х2=-1; х3=2; х4=0.
Запишем матрицу системы вместе с расширенной матрицей сразу поменяв уравнения местами: 3 уравнение поставим на 1 место в системе, 4 уравнение на 2 место, 1 уравнение на 3 место, 2 уравнение на 4 место.