Я буду очень вам благодарна ❤️
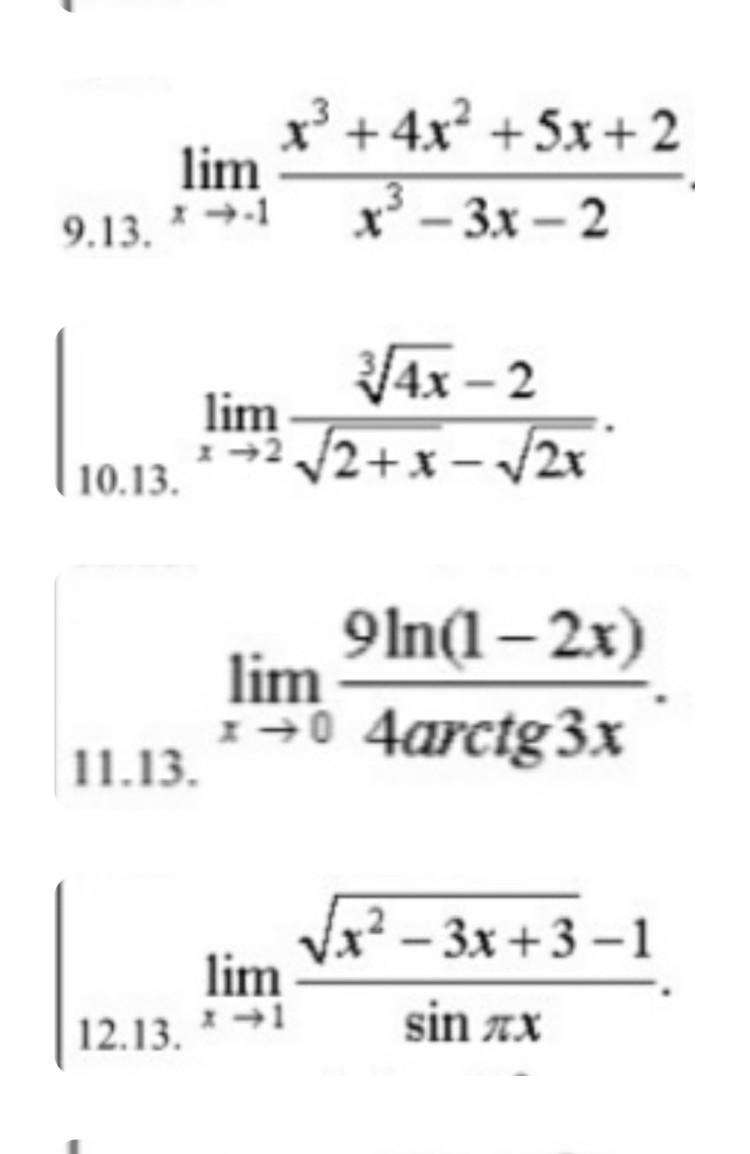
Ответы
Ответ:
Пошаговое объяснение:
9.13.
lim(x→-1)(x³+4x²+5x+2)/(x³-3x-2)=
=lim(x→-1)(x³+2x²+2x²+x+4x+2)/(x³+2x²-2x²+x-4x-2)=
=lim(x→-1)((x³+2x²+x)+(2x²+4x+2)/((x³+2x²+x)-(2x²+4x+2))=
=lim(x→-1)(x*(x²+2x+1)+2*(x²+2x+1))/((x*(x²+2x+1)-2*(x²+2x+1))=
=lim(x→-1)((x+1)²*(x+2))/((x+1)²*(x-2))=lim(x→-1)(x+2)/(x-2)=(-1+2)/(-1-2)=-1/3.
10.13.
lim(x→2)(∛(4x)-2)/(√(2+x)-√(2x))
Неопределённость 0/0. ⇒
Возьмём одновременно производную от числителя и знаменателя:
(∛(4x)-2)'=(2²/³*∛x)'=2²/³/(3√x).
(√(2+x)-√(2x))'=(1/(2√(x+2)-(√2/(2√x)) ⇒
lim(x→2)((2²/³)/(3∛x))/(1/(2√(x+2)-√2/(2√x))=
=lim(x→2)((2²/³)/((3*x²/³))/(1/(2√(x+2)-1/(√2√x))=
=(2²/³)/((3*2²/³)(3*(1/(2√(2+2))-1/(√2√2))=(2²/³)(2⁻²/³)/(3*(1/((2*√4)-(1/2))=
=(2⁰)/(3*((1/2²)-(1/2))=1/(3*((1/4)-(1/2))=1/(3*(-1/4))=-4/3.
11.13.
lim(x→0)(9*ln(1-2x)/(4*arctg(3x))
Неопределённость 0/0. ⇒
Возьмём одновременно производную от числителя и знаменателя:
(9*ln(1-2x))'=-9*2/(1-2х).
(4*arctg(3x))'=4/(1+(3x)²)=4*3/(3*(3x²+(1/3))=4/(3x²+(1/3)).
lim(x→0)(-9*2*(3x²+(1/3))/(4*(1-2x))=-(9/2)*(3*0²+(1/3))/(1-2*0)=
=(-9/2)*(1/3)/1=-3/2.
12.13.
lim(x→1)(√(x²-3x+3)-1)/sin(π*x)
Неопределённость 0/0. ⇒
Возьмём одновременно производную от числителя и знаменателя:
(√(x²-3x+3)-1)'=(2x-3)/(2*√(x²-3x+3)).
(sin(πx))'=π*cos(πx).
lim(x→1)(2x-3)/(2*√(x²-3x+3)*π*cos(πx)=(2*1-3)/(2*√(1²-3*1+3)*π*cos(π*1)=
=(2-3)/(2*√(1-3+3)*π*cosπ)=-1/(2*√1*π*(-1)=1/(2π).