Предмет: Математика,
автор: sashamimimi33
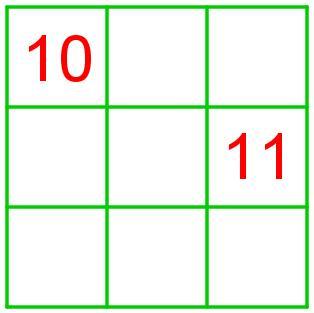
Запишите в свободные клетки квадрата числа 3, 4, 5, 6, 7, 8, 9 так, чтобы суммы чисел во всех строках, столбцах и на двух диагоналях были бы равными. Какое число будет записано в нижней строке слева?
Приложения:
Ответы
Автор ответа:
0
Ответ:
8
Пошаговое объяснение:
10__a___b
c___d __11
e___f___g
Сумма всех элементов равна 3+4+…+9+10+11=(3+11)*9/2=63.
Это также сумма сумм чисел в 3 строках => в каждой строке, столбце, диагонали сумма элементов равна 63/3=21.
Тогда:
a+b+c+d+e+f+g=63-10-11=42
d+g=a+b=c+e=11 => a+b+c+d+e+g=3*11=33 => f=42-33=9
10 __a___b
c___d___11
e___9___g
21=b+d+e≤6+7+8=21 => На местах b, d и е стоят числа 6, 7 и 8. Тогда на местах а, с и g стоят 3, 4 и 5 => a+c+g=3+4+5=12
a+d =12, c+d=10 => a-c=2. Т.к а и с могут принимать лишь значения 3, 4 и 5, a=5 и c=3 => d=12-5=7, e=11-3=8 => для b остается число 6, а для g - 4
10 __5___6
3___7___11
8___9___4
Похожие вопросы
Предмет: Математика,
автор: uis2807201072
Предмет: Українська мова,
автор: omagarbldanilacrazy
Предмет: Английский язык,
автор: Аноним
Предмет: Алгебра,
автор: катя3680
Предмет: Литература,
автор: asddsasda123321