Решите пожалуйста
В треугольнике ABC с углом,равным 100, проведена высота CH=4.Найдите угол CAB,если CB=8
Ответы
Так как не сказано, какой угол равен 100°, то в этой задаче это может быть как ∠С, так и ∠В , так и ∠А .
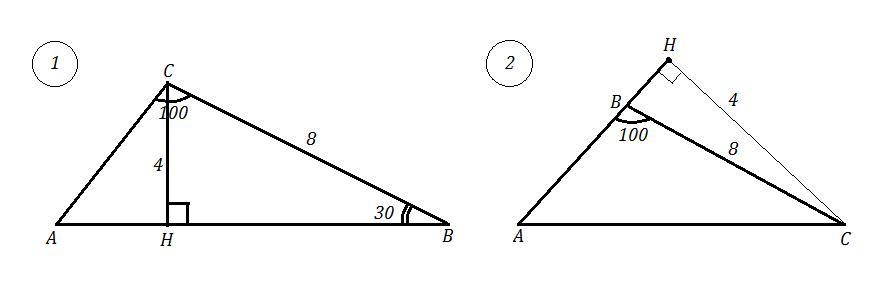
1) Дан ΔАВС , ∠С=100°, СН⊥АВ ⇒ ∠СНВ=90° , СН=4 , СВ=8 .
Так как ∠СНВ=90°, то ΔВСН - прямоугольный. В нём гипотенуза ВС=8, а катет СН=4, то есть катет равен половине гипотенузы. Значит угол, лежащий против катета СН равен 30°, то есть ∠СВН=30° .
Найдём угол А, учитывая, что сумма углов в ΔАВС равна 180°.
∠САВ=180°-∠С-∠В=180°-100°-30°=50° . См. рисунок.
2) ΔАВС , ∠В=100° , СН⊥АВ , СН=4 , СВ=8 .
Рассм. ΔСВН, ∠СНВ=90°, СН=4 , ВС=8 ⇒ ∠СВН=30° .
Но т.к. ∠В=100°, то смежный с ним угол должен быть равен 80°, а смежным углом является как раз ∠СВН.
Получили противоречие. Значит, ∠В не может быть равен 100° .
Аналогично, ∠А не может быть = 100°. См. рисунок.