Question

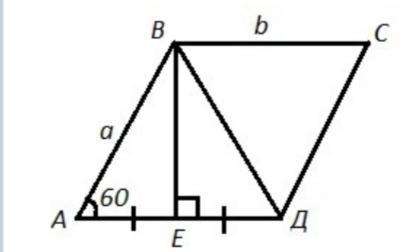
В параллелограмме АВСD угол А равен 60°.Высота ВЕ делит сторону AD на две равные части. Длина диагонали BD равна 10 см. Найдите периметр параллелограма.

Пожалуйста с чертежом

Answer 1

Ответ:

Объяснение:АВСД - параллелограмм , ∠А=60° , Р=48 см , ВЕ⊥АД , АЕ=ЕД .

Периметр параллелограмма Р=2·(a+b)=48 ⇒ a+b=24 .

АД+АВ=24 см.

Так как ВЕ - высота и АЕ=ЕД , то ΔАВД - равнобедренный: АВ=ВД .

Так как в равнобедренном ΔАВС один из углов равен 60°, то ΔАВС - равносторонний ⇒ АВ=ВД=АД ⇒ АД+АВ=2·АВ=24 , АВ=24:2=12 .

Диагональ ВД=АВ=12АВСД - параллелограмм , ∠А=60° , Р=48 см , ВЕ⊥АД , АЕ=ЕД .

Периметр параллелограмма Р=2·(a+b)=48 ⇒ a+b=24 .

АД+АВ=24 см.

Так как ВЕ - высота и АЕ=ЕД , то ΔАВД - равнобедренный: АВ=ВД .

Так как в равнобедренном ΔАВС один из углов равен 60°, то ΔАВС - равносторонний ⇒ АВ=ВД=АД ⇒ АД+АВ=2·АВ=24 , АВ=24:2=12 .

Диагональ ВД=АВ=12 см