Question

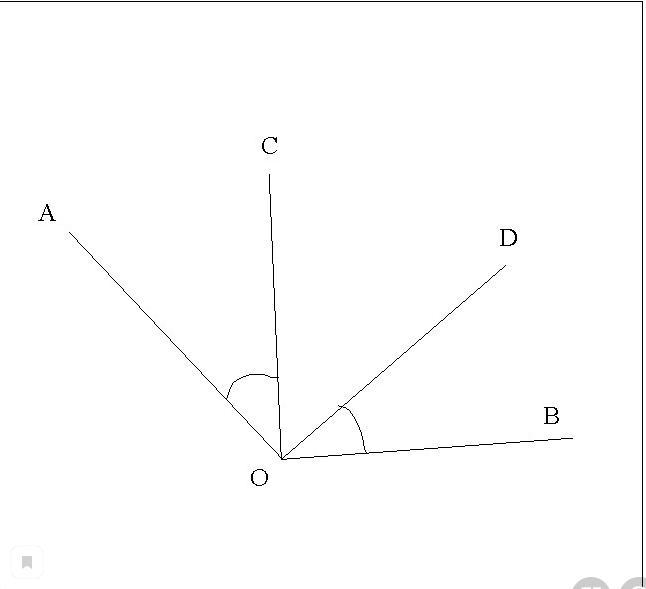
Даны два угла АОВ и ДОС с общей вершиной. Угол ДОС расположен внутри угла АОВ. Стороны одного угла перпендикулярны к сторонам другого. Найдите эти углы, если разность между ними равна прямому углу

Answer 1

Дано:

<AOB и <COD

<COD  внутри <AOB 

AO ┴ OD;  CO ┴ OB;

<AOB - <COD = 90°

Найти: <AOB и <COD.

Решение

Т.к . AO ┴ OD;  CO ┴ OB,

то <AOD = 90; <COB = 90°.

 <COD = <AOD  - <AOC

<COD = <COB  - <DOB

 

<COD = 90° - <AOC

<COD = 90° - <DOB

Получим

<AOC = 90° - <COD

<DOB = 90° - <COD

Следовательно <AOC = <DOB

 

2) По условию: <AOB - <COD = 90°

Но если от всего угла  <AOB отнять <COD, то останутся два равных угла  <AOC и <DOB, значит, это их сумма равна 90°.

<AOC + <DOB = 90° =>

<AOC = <DOB = 90°/2 = 45°

 

3) <COD = 90° - <DOB

<COD = 90° - 45°=45°

 

4) <AOB = <AOC + <DOB + <DOB

<AOB = 45° + 45° + 45° = 135°

Ответ: <AOB - 135°;  <COD =45°.