биссектриса параллелограмма ABCD делится делит его сторону BC на отрезки BK равно 19 см и KC на 10 см Найдите его периметр
Ответы
Ответ:
1). 96 см.; 2). 78 cм.
Объяснение: задача имеет 2 варианта решения
1). Дано: АВСD - параллелограмм, АК - биссектриса, ВК=19 см, КС=10 см. Найти Р (АВСD).
Рассмотрим ΔАВК - равнобедренный (∠ВАК=∠КАD по определению биссектрисы, ∠ВКА=∠КАD как внутренние накрест лежащие при ВС║АD и секущей АК), значит АВ=ВК=19 см.
АD=ВС=19+10=29 см; СD=АВ=19 см (как противоположные стороны параллелограмма)
Р=19*2+29*2=96 см.
2) Дано: АВСD - параллелограмм, DК - биссектриса, ВК=19 см, КС=10 см. Найти Р (АВСD).
Рассмотрим ΔDCК - равнобедренный (∠АDК=∠КDC по определению биссектрисы, ∠CКD=∠КDA как внутренние накрест лежащие при ВС║АD и секущей DК), значит KC=CD=10 см.
АD=ВС=19+10=29 см; СD=АВ=10 см (как противоположные стороны параллелограмма)
Р=10*2+29*2=78 см.
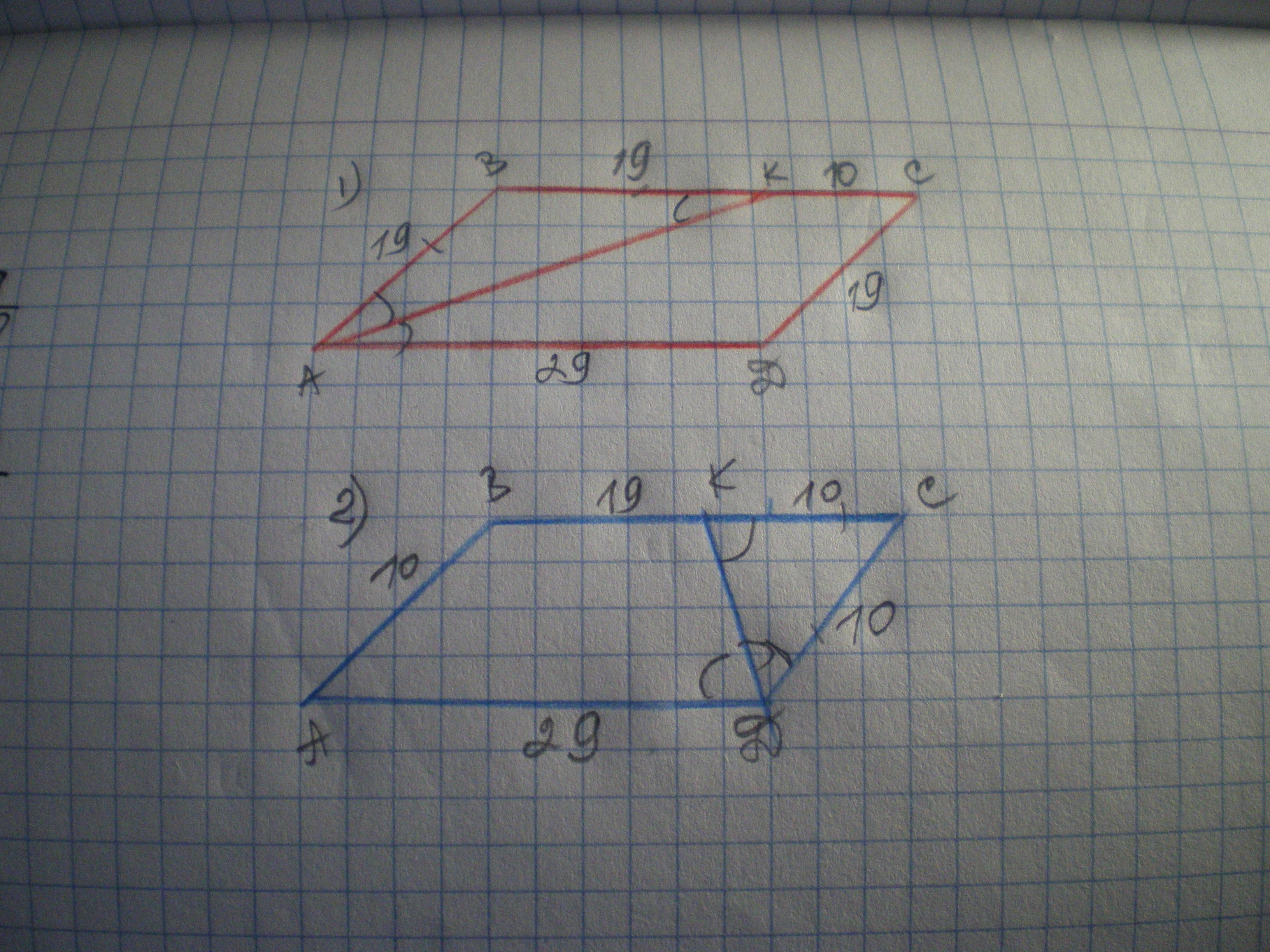
Ответ:
решение представлено на фото
Объяснение:
