Предмет: Алгебра,
автор: simmml
Решите, пожалуйста, один пример!!! 10 кл.
Приложения:
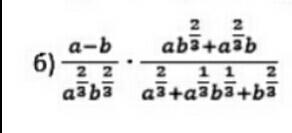
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Разложим а-b по формуле разности кубов
Пеобразуем
Получим
Похожие вопросы
Предмет: Русский язык,
автор: veronikalyamkh36
Предмет: Українська мова,
автор: dimadudnyk200833
Предмет: Математика,
автор: evelinaciksa
Предмет: Математика,
автор: barsillona
Предмет: Алгебра,
автор: iqqccdoj