Предмет: Алгебра,
автор: hfgh11
помогите пожалуйста
Приложения:
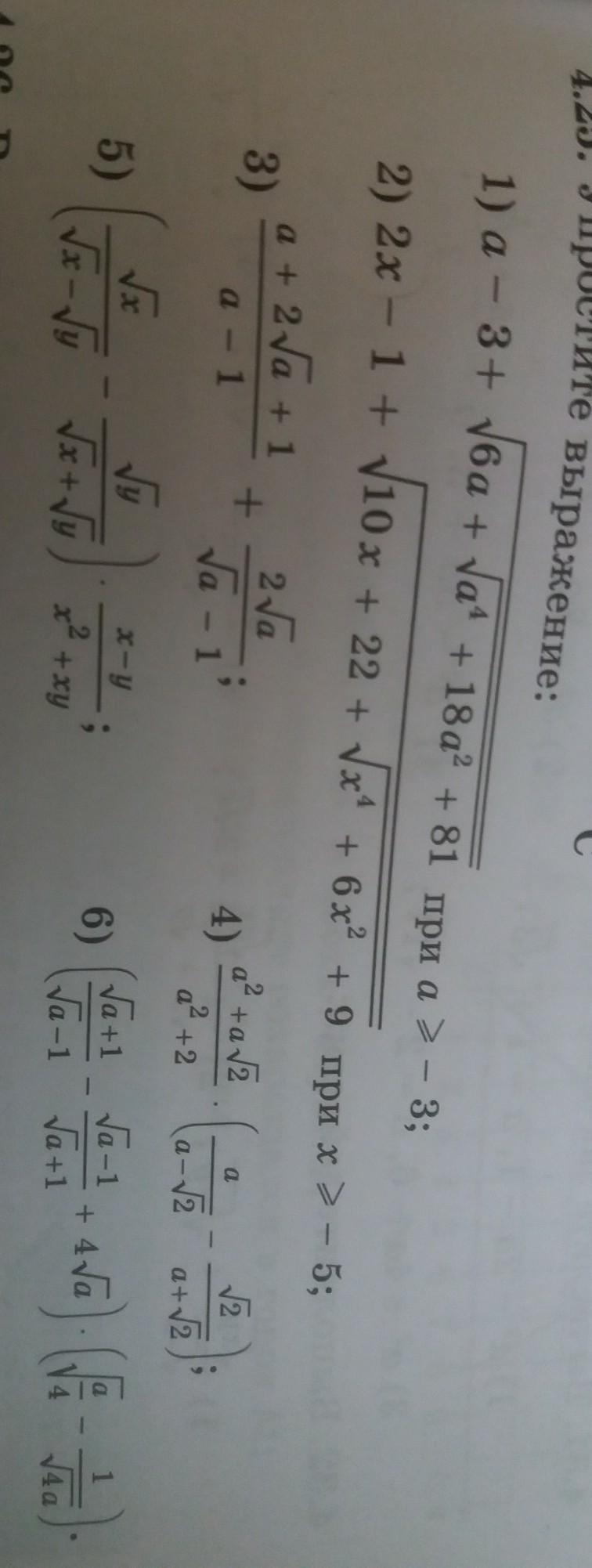
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Английский язык,
автор: okeanauwu74
Предмет: Русский язык,
автор: wefhckaixnf
Предмет: Геометрия,
автор: prostovika62
Предмет: Математика,
автор: Аноним
Предмет: История,
автор: настя5244