Предмет: Геометрия,
автор: MariannaWayMW
ДАЮ 50 БАЛЛОВ
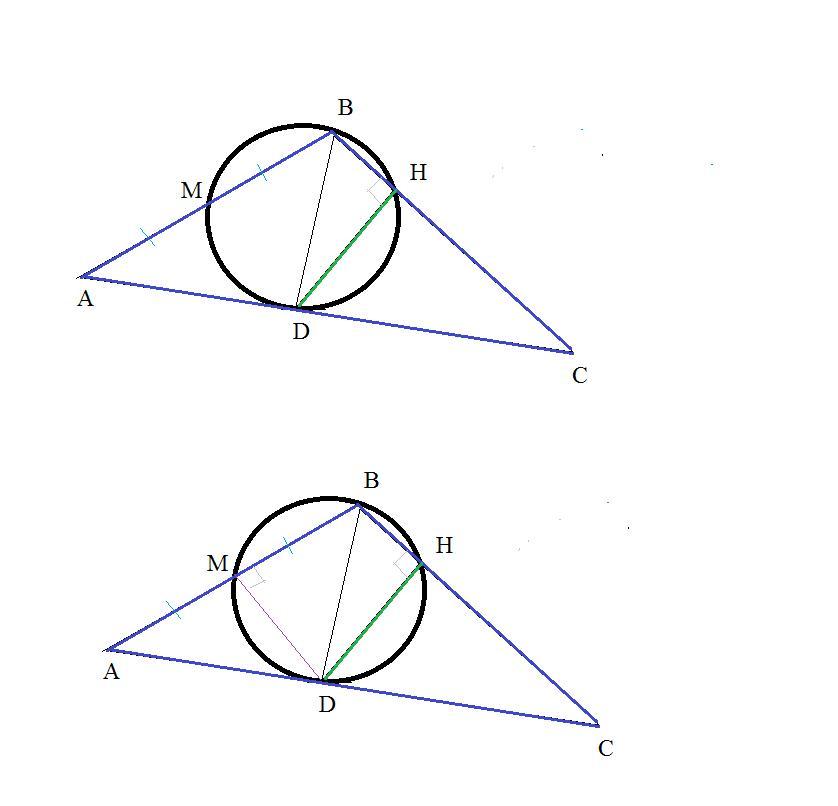
На стороне AC треугольника ABC выбрана точка D. Точка H-основание перпендикуляра, опущенного из точки D на сторону BC. Точка M-середина стороны AB. Известно, что точки B, M, D, H лежат на одной окружности. Докажите, что угол BDC в два раза больше угла BAC.
Ответы
Автор ответа:
2
Так как точки B, M, D, H лежат на одной окружности и DH⊥BC, то BD- диаметр и ∠ BMD=90°
Значит MD - медиана и высота треугольника АВD.
Δ АВD- равнобедренный.
∠MAD=∠MBD
∠BDC- внешний угол треугольника АВD, равен сумме внутренних с ним не смежных
∠BDC=∠MAD+∠MBD=2*∠MAD=2*∠BАС
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: ggffggff
Предмет: Информатика,
автор: arina2143
Предмет: Алгебра,
автор: yusubovaalsu777
Предмет: Математика,
автор: 29744
Предмет: Математика,
автор: 6665553