Вектора. Помогите за 100 баллов
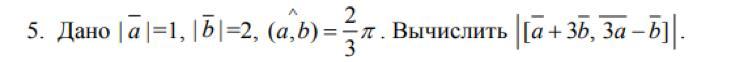
Ответы
Пусть вектор "а" по оси Ох, вектор"b" под углом 120 градусов.
Разложим векторы по осям координат: a = (1;0), b = (-1; √3).
Определяем заданные векторы:
x(a + 3b) = (1 + 3*(-1)) = 1 - 3 = -2,
y(a + 3b) = (0 + 3*(√3)) = 3√3. Вектор (a + 3b) = (-2; 3√3).
Модуль равен √(4 + 27) = √31.
x(3a - b) = (3*1 - 1)) = 3 - (-1) = 4,
y(3a - b) = (3*0 - √3) = -√3. Вектор (3a - b) = (4; -√3).
Модуль равен √(16 + 3) = √19.
Модуль векторного произведения равен произведению модулей векторов на синус угла между ними.
Находим угол между векторами.
Угол между вектором (a + 3b) и положительным направлением оси Ох равен abs(arc tg(-2/ 3√3)) + 90 = 21,0517 + 90 = 111,05172 градуса.
Угол между вектором (3a - b) и положительным направлением оси Ох равен abs(arc tg(√3/4)) = 23,41322 градуса.
Итого угол равен 111,05172 + 23,41322 = 134,46494 градуса.
Ответ: √31*√19*sin(134,46494) = 17,320508.
Такой же ответ получим при использовании координат векторов.
Произведение векторов
a × b = {aybz - azby; azbx - axbz; axby - aybx}
Векторное произведение 0 0 -17,32050808
Модуль 17,32050808.