Предмет: Алгебра,
автор: МатематическийМозг
Найдите площадь фигуры, ограниченной линиями.
Приложения:
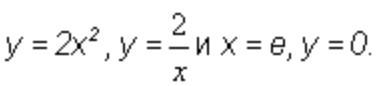
Аноним:
Какой ответ?
Сейчас попробую через двойные интегралы решить
5 ответов дано (тест ведь) 2.5; 2 2/3; 2 1/3; 1.5; 2
через двойные интегралы вышло 2 + 2/3
т.е. ответ 2 2/3
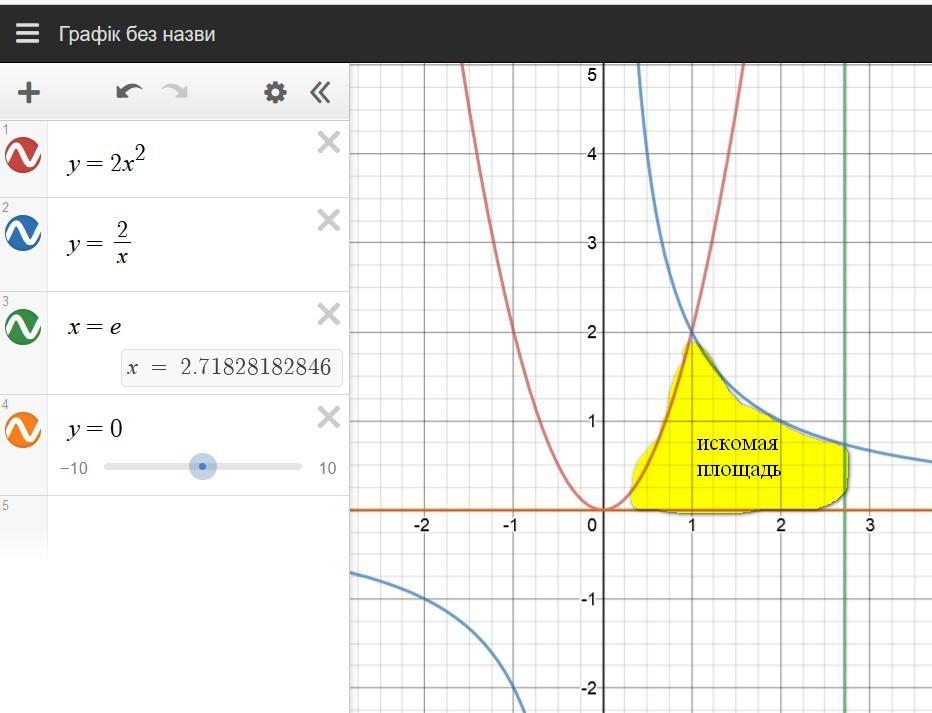
А с чего Вы взяли, что площади не существует? Если построить графики, то видно, что область имеет ненулевую площадь
Ненулевую и конечную*
Я не строил графики... Потом уже построил
Поторопился с точкой пересечения.
Почему пустое множество? Площадь существует. И двойные интегралы здесь не нужны
Ответы
Автор ответа:
3
Точки пересечения двух графиков: y = 2x² и y = 2/x:
2x² = 2/x
x³ = 1
x = 1
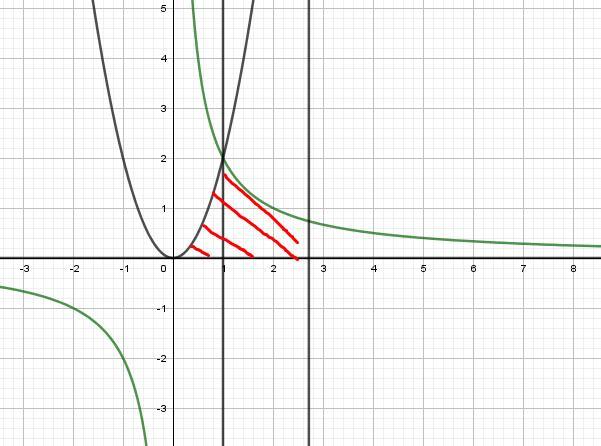
Далее построив графики и разобьем на две части прямой x = 1.
Площадь ограниченной линиями
кв. ед.
Приложения:
Автор ответа:
2
Если будут какие-нибудь вопросы — задавайте. Если мой ответ оказался полезен, ставьте «спасибо» и отмечайте его как «лучший ответ».
Приложения:

Похожие вопросы
Предмет: Алгебра,
автор: ballredwort35
Предмет: Математика,
автор: dracenaanastasia
Предмет: Алгебра,
автор: angelina0267
Предмет: Математика,
автор: tommy8hilfiger
Предмет: Математика,
автор: mariyamerlin1