Предмет: Алгебра,
автор: VALERIADIAMANDIS
Решить два предела(матанализ)
Приложения:
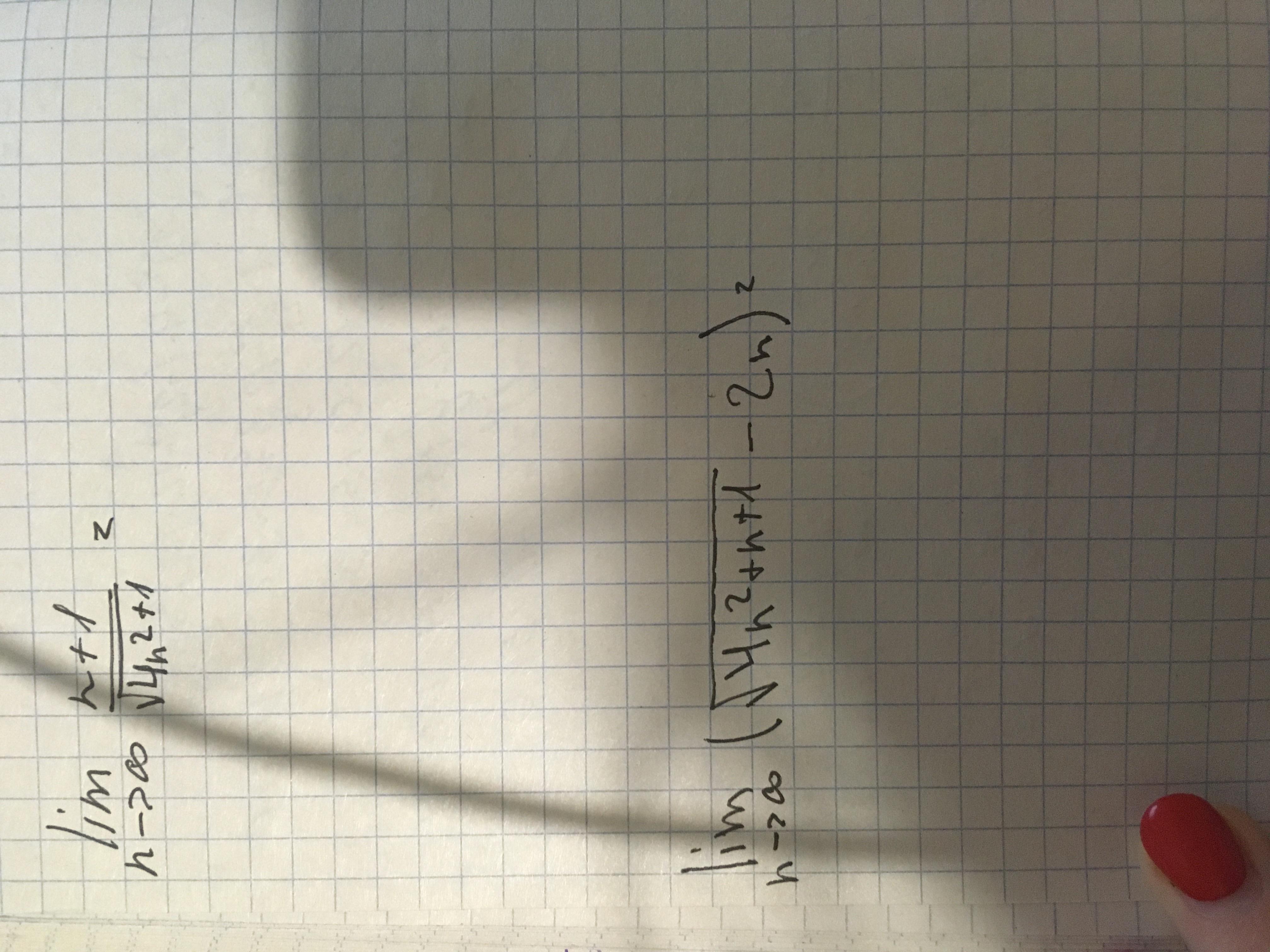
Ответы
Автор ответа:
0
rusfiz:
во втором выражение в скобках стоит в квадрате
нет квадрата. Знак равно. Так же как и в первом пределе. Вы же не поставили квадрат над дробью...
Похожие вопросы
Предмет: Русский язык,
автор: 7Linda7
Предмет: Химия,
автор: FinitiYiti681
Предмет: Литература,
автор: nazirkanybekov
Предмет: География,
автор: QWE7300